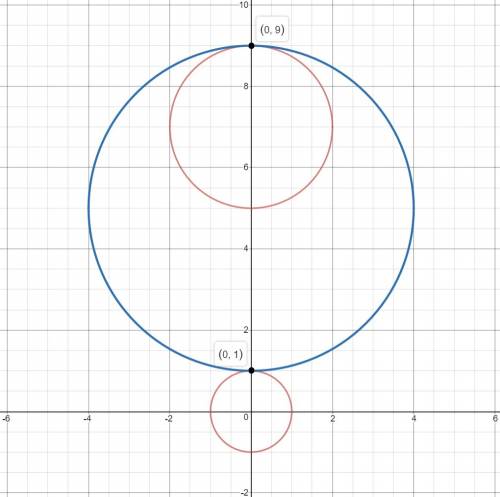
Окружность №1: x²+y²=1. Центр (0; 0), радиус 1.
Окружность №2: x²+(y-7)²=4. Центр (0; 7), радиус 2.
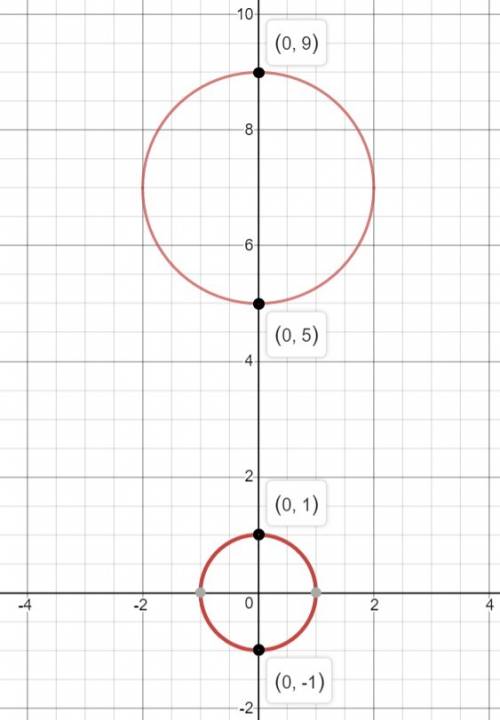
Для удобства и полного понимания ситуации строим данные окружности (изображение 1). Рассмотрим все возможные варианты:
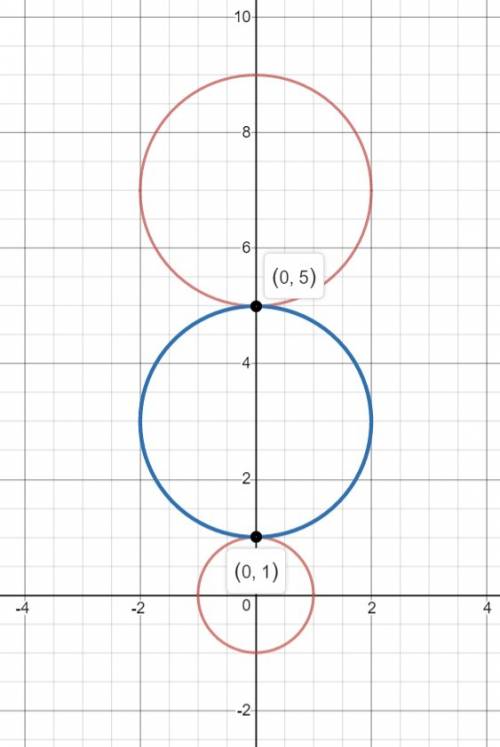
1) Окружность касается обоих данных окружностей внешним образом (изображение 2). В таком случае ее центр (0; 3), радиус 2.
x²+(y-3)²=4
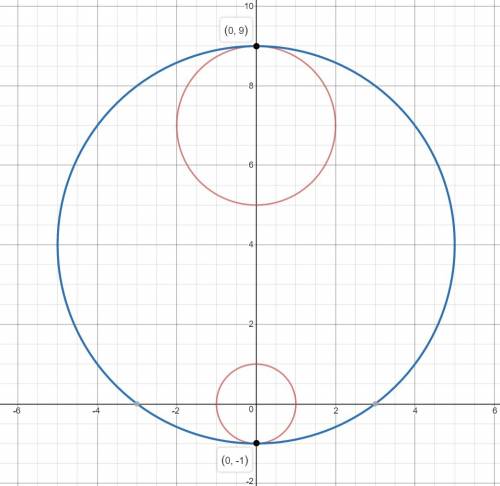
2) Окружность касается обоих данных окружностей внутренним образом (изображение 3). В таком случаем ее центр (0; 4), радиус 5.
x²+(y-4)²=25
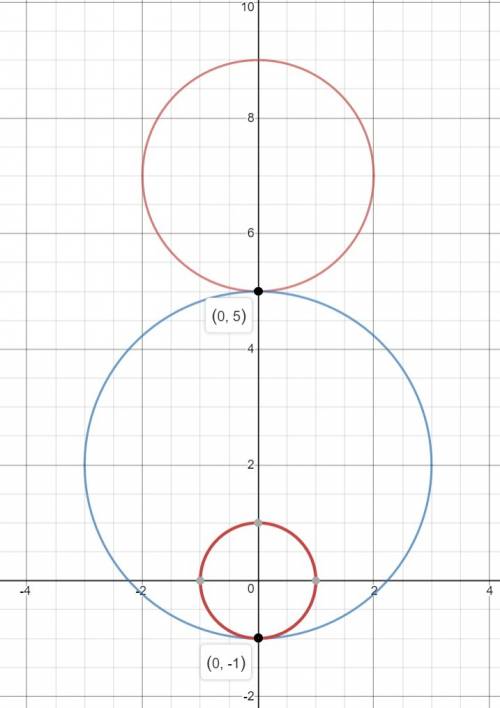
3) Окружность касается первой окружности внутренним образом, второй внешним (изображение 4). В таком случае ее центр (0; 2), радиус 3.
x²+(y-2)²=9
4) Окружность касается первой окружности внешним образом, второй внутренним (изображение 5). В таком случае ее центр (0; 5), радиус 4.
x²+(y-5)²=16
Объяснение:
Уравнение окружности имеет вид:
(x-x0)²+(y-y0)²=r²
Где (х0;у0) - координаты центра. r- радиус.
Подставив вместо х и у координаты данных точек получаем систему трех уравнений с тремя неизвестными:
для упрощения записи, вместо х0 напишу х, а вместо у0 напишу у:
(-3-x)²+y²=r²
(1-x)²+(3-y)²=r²
(5-x)²+y²=r²
вычтем из первого уравнения третье:
(-3-x)²-(5-x)²=0
9+6x+x²=25-10x+x²
16x=16
x=1
тогда получаем :
16+y²=r²
(3-y)²=r²
16+y²-(3-y)²=0
16+y²=9-6y+y²
6y=-7
y=-7/6
Тогда r²=820/49
Итак уравнение окружности имеет вид:
(x-1)²+(y+7/6)²=820/49
ответ: 18π см. 56,52 см.
Объяснение:
Сторона треугольника а= 6√3 см
R описанной окружности R= a/√3 = (6√3)/√3 = 6 см.
r вписанной r=a√3/6 = (6√3*√3)/6 = 3 см.
(См. скриншот).
Длина окружности C=2πR и c=2πr. Тогда
С+с = 2πR+2πr = 2π(R+r) =2*π(6+3) = 18π см. =>
или
С+с=2*3,14*9=6.28*9 = 56,52 см.