
1) 3/5+2/7 = 5/12(cм) вторая сторона
2)3/5+9/14= 11/19(см) третья сторона
Пошаговое объяснение:
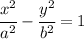 , где а и b - полуоси гиперболы
, где а и b - полуоси гиперболы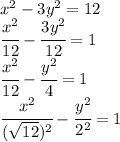
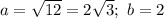
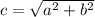
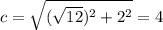
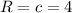
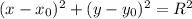 , где
, где 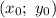 - центр окружности, R - ее радиус
- центр окружности, R - ее радиус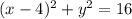
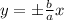
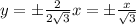
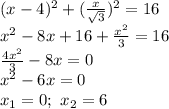
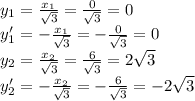
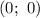 ;
; 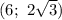 ;
; 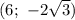
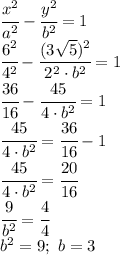
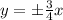
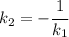
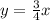 таким коэффициентом является число
таким коэффициентом является число 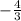 , а для прямой
, а для прямой 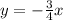 - число
- число 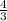
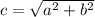
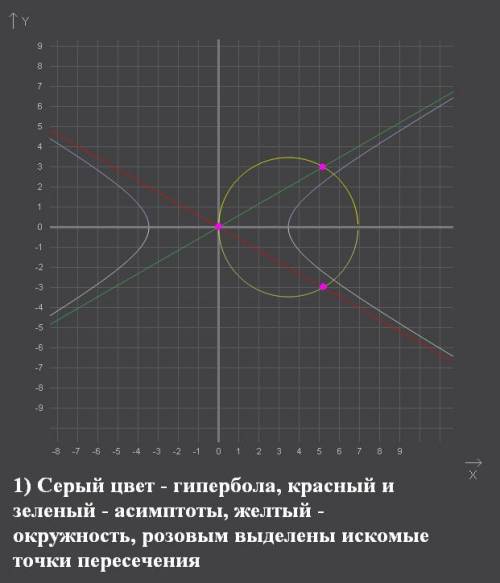
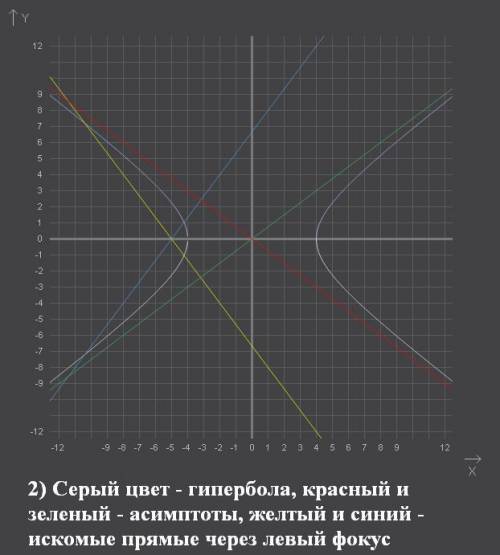
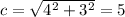 , следовательно через точку (-5; 0) нужно провести искомые прямые
, следовательно через точку (-5; 0) нужно провести искомые прямые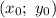 с заданным угловым коэффициентом k имеет вид:
с заданным угловым коэффициентом k имеет вид: 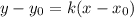
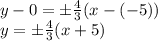
Первоначально в бригаде было x рабочих, которые работали по y часов в день.
Производительность всей бригады 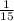 всей работы в день или
всей работы в день или  всей работы в час.
всей работы в час.
Производительность одного рабочего 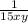 всей работы в час.
всей работы в час.
Если бригадир наймет девять дополнительных рабочих, и при этом в день бригада будет работать на 2 часа меньше, то работа будет выполнена за 12 дней, то есть
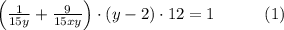
Если бригадир уволит пятерых рабочих из первоначального состава бригады, то, чтобы окончить работу за 20 дней, бригаде придётся трудиться на 2 часа в день больше, то есть
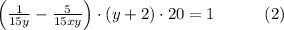
Составим и решим систему уравнений (1) и (2):

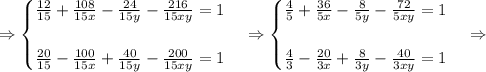
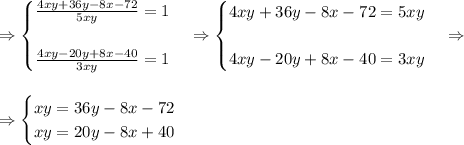
Вычтём из первого уравнения второе:
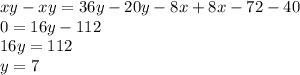
Подставим значение y в любое из двух уравнений систему (например, во второе) и вычислим x:
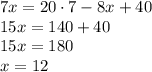
Тогда
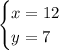
ответ: первоначально в бригаде было 12 рабочих, которые работали по 7 часов в день.
1
24+18=42 вторая сторона
42÷2=21 третья сторона
24+21+42=87 периметр
2
9+7+7=23
так как боковые стороны равны
3
19-7=12
12÷2=6 боковая сторона
4
42÷3=14 одна из сторон , а так ка все стороны равны то посчитаев её за основание
58-14=44
44÷2=22 одна из боковых сторон
Пошаговое объяснение: