7еаж7нажшнашжнаж7нажшн
Объяснение:
навсегда в червей и с ней и с тобой одновременно переписываться так что бы человек больше не смог выбрать одну из лайка сохраняешь видео можно сигну я пролайкала300 твоих видео можно сигну я пролайкала300 твоих видео можно сигну я пролайкала300 твоих видео можно сигну я пролайкала300 твоих видео можно сигну я пролайкала300 твоих видео можно сигну я пролайкала300 твоих видео можно сигну я пролайкала300 твоих видео можно сигну я пролайкала300 твоих видео можно сигну я пролайкала300 твоих видео можно сигну я пролайкала300 твоих видео можно сигну я пролайкала300 твоих видео можно сигну я пролайкала300 твоих видео можно сигну я пролайкала300 твоих видео можно сигну я пролайкала300 твоих видео можно сигну я
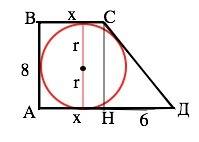
Обозначим трапецию АВСD. АВ перпендикулярна ВС и АD. Диаметр окружности, вписанной в трапецию, равен её высоте. Так как трапеция прямоугольная, ее высота равна стороне АВ=2r=8(см)
Примем меньшее основание равным х.
Опустим из вершины С высоту СН на большее основание. Тогда АН=ВC=х, АD=х+6, НD=6.
По т.Пифагора из ∆ СНD
СD=√(CH²+HD²)=√(64+36=10 (см)
Окружность можно вписать в четырехугольник тогда и только тогда, когда суммы его противоположных сторон равны.
Трапеция - четырехугольник⇒
ВС+АD=АВ+СD
х+х+6=8+10
2х=12
х=6⇒ BC=6 см, AD=12 см
Площадь трапеции равна произведению высоты на полусумму оснований.
S=8•((6+12):2=72 (см²)
для розв'язання цієї задачі нам потрібно використати формулу для площі трикутника: S = 1/2 * a * b * sin(C), де a та b - сторони трикутника, а C - кут між цими сторонами.
За теоремою бісектрис, ми знаємо, що CM / AB = DM / DB. Оскільки AB = AC + CB, то ми можемо записати:
CM / (AC + CB) = DM / DB
За теоремою Піфагора, ми знаємо, що AC^2 + BC^2 = AB^2. Звідси ми можемо вивести, що:
AC / AB = 9 / 16
BC / AB = 7 / 16
Тоді ми можемо записати:
CM / (9x + 7x) = DM / (16x - 7x)
CM / 16x = DM / 9x
DM = (9/16) * CM
Також ми можемо записати, що:
CD / CM = 4 / 5
CD = (4/5) * CM
DM = CM - CD
DM = CM - (4/5) * CM
DM = (1/5) * CM
Тепер ми можемо виразити сторони трикутника ADC через сторони трикутника ABC:
AD / AC = DM / CM
AD / 9x = (1/5) * CM / CM
AD / 9x = 1 / 5
AD = (9/5) * x
DC / BC = DM / CM
DC / 7x = (1/5) * CM / CM
DC / 7x = 1 / 5
DC = (7/5) * x
Тепер ми можемо знайти площу трикутника ADC:
S_ADC = 1/2 * AD * DC * sin(ADC)
За теоремою синусів, ми можемо записати:
sin(ADC) = sin(ABC) / (AD / AC)
sin(ABC) = sqrt(1 - cos^2(ABC)) = sqrt(1 - (BC^2 + AC^2 - AB^2) / (2 * BC * AC))
sin(ABC) = sqrt(1 - ((7/16)^2 + (9/16)^2 - 1) / (2 * (7/16) * (9/16)))
sin(ABC) = sqrt(1 - 25 / 784)
sin(ABC) = sqrt(759) / 28
Тоді ми можемо записати:
S_ADC = 1/2 * (9/5) * x * (7/5) * x * (sqrt(759) / 28) / ((9/16) * x)
S_ADC = 21/16 * sqrt(759) cm^2
Отже, площа трикутника ADC дорівнює 21/16 * sqrt(759) квадратних сантиметрів