35114225 35113996
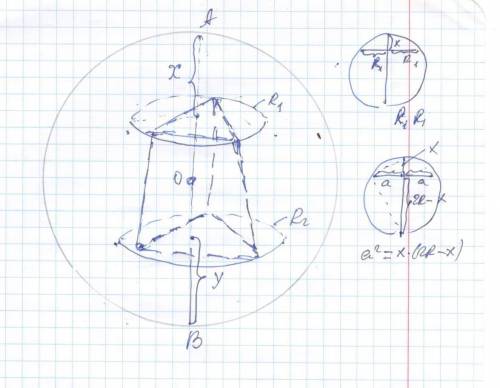
Высота усеченной правильной пирамиды равна 7 см, а длины сторон оснований 3√3 см и 4√3 см. Вычислить радиус описанного шара
R₁ =3√3* √3 /3 = 3 * * * R =(a√3/2)*2/3 =(a√3)/3 * * *
R₂ =4√3* √3 /3 = 4
R₁² = x (2R - x) ⇔x² - 2Rx + 9 = 0 ⇒ x₁ =R -√(R²- 9)
Маленький кусок диаметра x₁ =12 (между основания со стороной 3√3 и поверхностью шара) ( большой кусок x₂=R+√(R²- 9) )
Аналогично
R₂² = y (2R -y) ⇔ y² - 2Ry + 16=0 ⇒ y ₁ = R -√(R²- 16 )
x₁+ H + y₁ = 2R ⇔ R -√(R²- 9) + 7 + R -√(R²- 16) = 2R ⇔
R -√(R²- 9) + 7 + R -√(R²- 16) =2R ;
√(R²- 9) + √(R²- 16) =7 * * * ясно R =5 * * *
примитивное иррациональное уравнение ,необяз. замена t =R² > 0
√(t- 16) = 7 - √(t - 9) ⇔ t- 16 =49 -14√(t - 9) + t -9⇔ 14√(t - 9) =56 ⇔
t - 9 = 4² ⇔ t =25 * * * 3 ; 4 ;5 * * *
R² =25 ⇒ R = 5 ( R = -5 построенное решение )
ответ : 5 см .
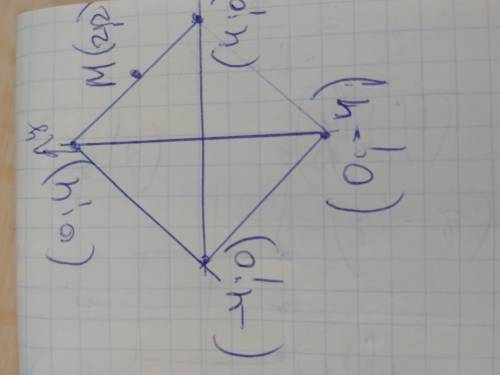
(4;0), (-4;0), (0;-4),(0;4)
Объяснение:
Оси координат - оси симметрии квадрата, но у квадрата возможны 4 оси симметрии. Это либо средние линии, либо диагонали. Т.к. Середина одной из сторон т.М(2;2), то оси симметрии - не средние линии, а диагонали, иначе середина стороны лежала бы на одной из осей и имела в координатах ноль. Значит ось х и у проходят через диагонали квадрата. Если половина значения х вершины =2, то х вершины =4, половина значения у вершины =2, то у вершины =4.
Вершинами квадрата являются точки (4;0), (-4;0), (0;-4),(0;4)
ответ: ∠AOB=135°
S(AOB)=2.5
Объяснение:
AB= 5 (AB² =AC²+BC² ; 3²+4²=5²)
Пусть N -точка касания окружности катета АС, М- точка касания катета СВ, а L - гипотенузы АВ.
Пусть LA=NA=x => CN=CM=3-x => BM=BL=4-(3-x)=1+x
=> AB=LA+BL=1+x+x=5
2x=4 => x=2 => NO =CM=NC=1 ( O- центр вписанной окружности)
По т Пифагора AO= \sqrt{AN^2+NO^2} =\sqrt{5}
Аналогично ВО =\sqrt{BM^2+MO^2} =\sqrt{9+1} =\sqrt{10}
Применим т косинусов к треугольнику АОB
AB²= AO²+BO²-2AO*BO*cos AOB
25=10+5-2*√10*√5*cosAOB => -2√50*cos AOB=10
cos AOB= -1/√2 => ∠AOB=135°
S(AOB)= 0.5*AB*LO= 0.5*5*1=2.5