На рисунке обозначены:
ABC - Основание пирамиды
OS - Высота
KS - Апофема
OK - радиус окружности, вписанной в основание
AO - радиус окружности, описанной вокруг основания правильной треугольной пирамиды
SKO - двугранный угол между основанием и гранью пирамиды (в правильной пирамиде они равны)
Важно. В правильной треугольной пирамиде длина ребра (на рисунке AS, BS, CS ) может быть не равна длине стороны основания (на рисунке AB, AC, BC). Если длина ребра правильной треугольной пирамиды равна длине стороны основания, то такая пирамида называется тетраэдром (см. ниже).
Свойства правильной треугольной пирамиды:
боковые ребра правильной пирамиды равны
все боковые грани правильной пирамиды являются равнобедренными треугольниками
в правильную треугольную пирамиду можно как вписать, так и описать вокруг неё сферу
если центры вписанной и описанной вокруг правильной треугольной пирамиды, сферы совпадают, то сумма плоских углов при вершине пирамиды равна π (180 градусов) , а каждый из них соответственно равен π / 3 (пи делить на 3 или 60 градусов ).
площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
вершина пирамиды проецируется на основание в центр правильного равностороннего треугольника,, который является центром вписанной окружности и точкой пересечения медиан
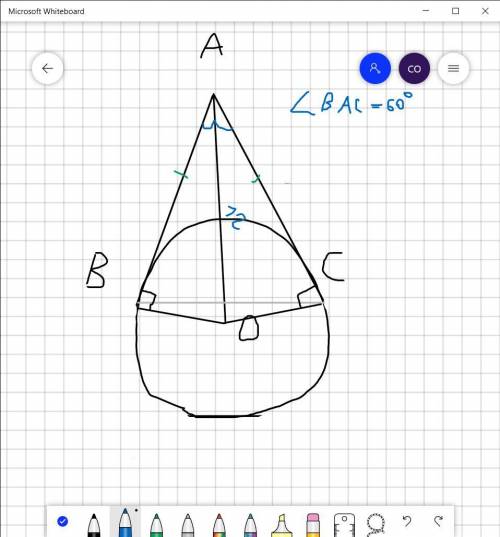
Відрізки двох дотичних, що виходять із однієї точки, рівні. АВ=АС, тому трикутник АВС рівнобедрений
Трикутники АВО і АСО рівні за трьома сторонами (ОВ=ОС як радіуси одного кола, АО-спільна, АВ=АС як зазначалося раніше)
Тому і відповідні кути рівні, а саме <BAO=<OAC=<ВАС/2=60°/2=30°
Знайдемо радіус через трикутник АОВ. Радіус, проведений до точки дотику дотичної і кола, перпендикулярний до цієї дотичної, тому <ОВА=90° і трикутник АОВ прямокутний
ОВ лежить навпроти кута 30°, а АО гіпотенуза, тому радіус удвічі менше за АО
R=OB=12/2=6 см
Чтобы найти площадь заштрихованной области Sтреугольник надо минусанут надо Sокружность.
Как нам это сделать?
Нам дан квадрати его площадь.
S=a² a=8
Нарисовав картинку мы видим,что половина диагонали равна к радиусу
d=√(8²+8²)=√128=8√2
r=8√2 /2= 4√2
Теперь можно найти Sокружность:
S=pi*r²=3.14*32=100.48
Как найти Sтреугольник?
Есть формула вписанной окружности
r=Sтреугольник/ p
S=pr
S=4√2p
p=P/2
Как найти сторону, чтобы найти периметр?
Есть формула для окружности вписанной в правильный треугольник.
a=2√3*r
а=8√6
P=8√6* 3/2=12√6
p=12√6 /2= 6√2
S=4√2*6√2=48
Sштрих= 100.48-48= 52.48м²