
1. 13 см и 13 см
2. AM:AB=1:3 и MB:AB=2:3
Объяснение:
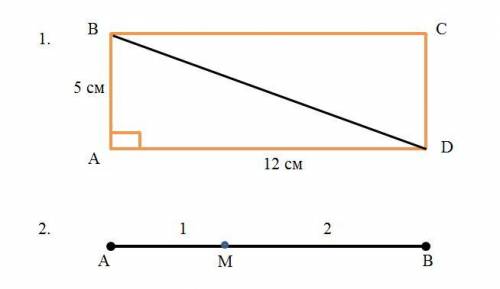
1. Диагонали прямоугольника равны и поэтому достаточно определить длину одной из них, например BD (см. рисунок).
Так как диагональ прямоугольника делит прямоугольник на два прямоугольных треугольника, то для прямоугольного треугольника применим теорему Пифагора:
BD²=AB²+AD² = (5 см)²+(12 см)² = 25 см² + 144 см² = 169 см²=(13 см)²
Отсюда
BD=13 см.
2. Так как отношение AM:MB=1:2, то MB=2·AM. Тогда
AB=AM+MB=AM+2·AM=3·AM.
Поэтому
AM:AB=AM:(3·AM)= 1:3
MB:AB=(2·AM):(3·AM)= 2:3
Сторона квадрата а = квадратному корню из числа Q . Диаметр окружности, описанной около квадрата, по теореме Пифагора
d = квадратному корню из произведения2а в квдрате = корню квадратному из произведения 2Q. Радиус окружности в два раза меньше диаметра, поэтому
R =частному d/2= частному корня квадратного из произведения2Q/2 . Длину стороны правильного треугольника, вписанного в ту же окружность, выразим через радиус окружности: a=Rумноженное на квадратный корень из 3. Площадь правильного треугольника вычислим по формуле: S= частному произведения а на корень из3/4. После подстановок окончательный результат частное произведения 3Qумноженное на корень из3деленное на 8
ответ: ;