|AC| = 10 см.
Объяснение:
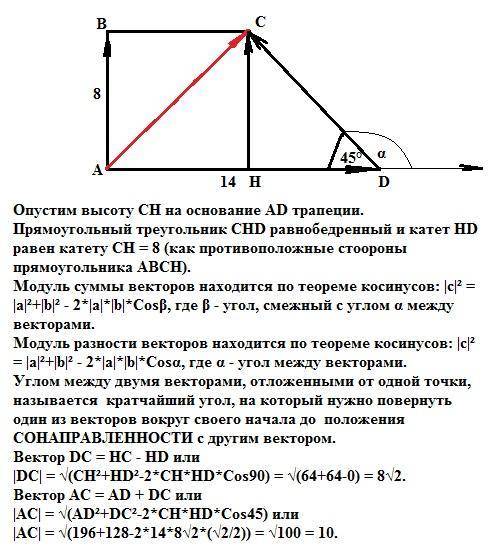
Опустим высоту СН на основание AD трапеции.
Прямоугольный треугольник СНD равнобедренный и катет HD равен катету СН = 8 (как противоположные стоороны прямоугольника АВСН).
Модуль суммы векторов находится по теореме косинусов: |c|² = |a|²+|b|² - 2*|a|*|b|*Cosβ, где β - угол, смежный с углом α между векторами.
Модуль разности векторов находится по теореме косинусов: |c|² = |a|²+|b|² - 2*|a|*|b|*Cosα, где α - угол между векторами.
Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения СОНАПРАВЛЕННОСТИ с другим вектором. Итак,
Вектор DC = НС - HD или
|DC| = √(CH²+HD²-2*CH*HD*Cos90) = √(64+64-0) = 8√2.
Вектор АС = AD + DC или
|AC| = √(AD²+DC²-2*CH*HD*Cos45) или
|AC| = √(196+128-2*14*8√2*(√2/2)) = √100 = 10.
ответ: Длина вектора (модуль) АС = 10 см.
Задача №1.
на проекции видно, что треугольник АОВ - равнобедренный ОА = ОВ =R =10 см
основание треугольника АВ= 12 см (это сторона квадратного сечения - она равна высоте h= 12 см)
расстояние от оси цилиндра до секущей плоскости - высота d
высота d делит сторону АВ на равные части , тогда АК=АВ/2=12/2= 6 см
тогда по теореме Пифагора
d^2 = OA^2 - AK^2= R^2 - AK^2 = 10^2 - 6^2 = 64= 8^2
d= 8 см
ответ 8 см расстояние от оси цилиндра до секущей плоскости.
Задача №2
Из правил сервиса: "Пользователи признают, что задания, которые содержат большое количество задач, требующих решения, должны быть разделены на два или несколько заданий и в таком виде добавлены в Сервис для других Пользователей. То есть в одном задании не может быть несколько задач".