Сумма двух проттивоположных сторон описанного четырёхугольника равна 10 см а его площадь-12см в квадрате . найдите радиус окружности, вписанной в этот четырёхугольник.

👇

Увидеть ответ

Ответ:

ZelyakAnna

11.12.2021

У описанного четырехугольника суммы противоположных сторон равны

Пусть задан четырехугольник ABCD

значит AB+CD=BC+AD=10 см

Площадь четрырехуольника равна

S=1\2*AB*r+1\2*BC*r+1\2*CD*r+1\2*AD*r=

1\2*(AB+CD)*r+1\2*(BC+AD)*r=1\2*2*(AB+CD)*r=(AB+CD)*r

Радиус вписанной окружности равен

r=S\(AB+CD)

r=12\10=1.2

ответ: 1.2 см

4,4(96 оценок)

Открыть все ответы

Ответ:

MasterHacker

11.12.2021

Дано: АВСD - параллелограмм, АС=ВD

Доказать: АВСD - прямоугольник.

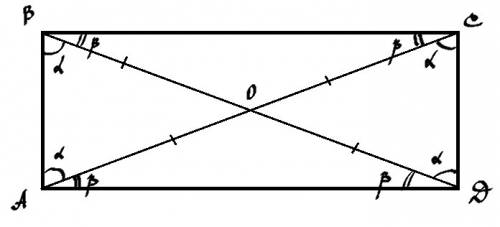
Доказательство: В параллелограмме диагонали точкой пересечения делятся пополам. Т.к. диагонали равны, то ВО=ОС=АО=ОD (смотри рисунок).

ΔАВО и ΔОСD равнобедренные.

АВ=СD, ВО=ОС, АО=ОD ⇒ ΔАВО = ΔОСD (по трем сторонам)

Значит ∠ОВА=∠ВАО=∠ОСD=∠CDО=α.

ΔВОС и ΔАОD равнобедренные

ВС=АD, ВО=ОА, СО=OD ⇒ ΔВОС = ΔАОD (по трем сторонам)

Значит ∠CBO=∠BCO=∠OAD=ODA=β

∠СВА=α+β

∠ВАD=α+β

∠АDС=α+β

∠DСВ=α+β

В четырехугольнике сумма всех углов 360°.

∠СВА+∠ВАD+∠АDС+∠DСВ=(α+β)+(α+β)+(α+β)+(α+β)=4(α+β)=360°

4(α+β)=360°

α+β=360°:4

α+β=90°

∠СВА=α+β=90°

∠ВАD=α+β=90°

∠АDС=α+β=90°

∠DСВ=α+β=90°

Все углы в параллелограмме АВСD прямые, следовательноа АВСD – прямоугольник.

Докажите что если в параллелограмме диагонали равны то параллелограмм является прямоугольником ?

4,7(51 оценок)

Ответ:

Denaz

11.12.2021

Для построения треугольника недостаточно данных; нужны еще один из острых углов или высота треугольника.
Как известно, длина медианы прямоугольного треугольника равна половине длины его гипотенузы и равна длине радиуса, описанного вокруг этого треугольника.
Начертим гипотенузу АВ. По известной методике деления отрезка на две равные части находим ее середину О.
Для этого из концов А и В чертим полуокружности радиусом больше половины отрезка, точки их пересечения соединяем прямой.
Эта прямая делит АВ пополам и является перпендикуляром к АВ.
Место пересечения обозначим О ( ОА=АА1, как дано в задаче)
Вариант 1.
Соединяем О с точкой пересечения перпендикуляра и окружности. Это вершина С. Соединяем А, В, С. Получен равнобедренный прямоугольный треугольник АВС.
Вариант 2.
Из А, как из вершины откладываем известные острый угол, проводим его сторону до пересечения с окружностью. Точка пересечения - вершина угла С. АВС - искомый треугольник.
Вариант 3.
Из А или В возводим перпендикуляр, равный заданной длине высоты треугольника. Проводим параллельно АВ прямую. Все ее точки равноудалены от АВ.
Точку пересечения прямой и окружности обозначим С.
Треугольник АВС - искомый.

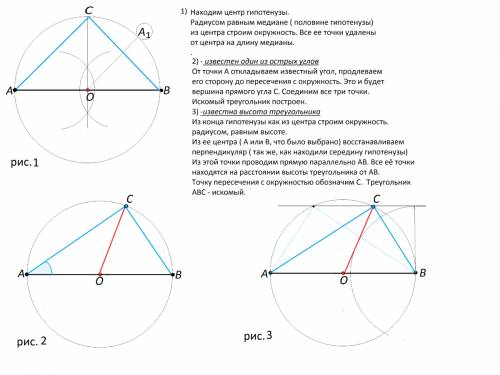
Построить треугольник abc по гипотенузе ab и медиане aa1. , , надо