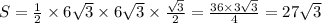10√3 см
Объяснение:
Длинная наклонная - с углом 30° с плоскостью
Высота равна половине длинной наклонной
h = l₁/2 = 15/2 см
Теорема Пифагора для второй наклонной l₂ как гипотенузы, высоты h как катета и проекции p₂ как катета против угла в 30°
l₂² = h² + p₂²
l₂² = h² + (l₂/2)²
l₂² = h² + l₂²/4
3/4*l₂² = h²
l₂ = 2h/√3
l₂ = 2*15/2/√3 = 5√3 см
Угол между наклонными 90°
Расстояние d между основаниями наклонных - гипотенуза, наклонные - катеты
l₁² + l₂² = d²
d² = 15² + (5√3)²
d² = 225 + 25*3 = 300
d = √300 = 10√3 см
ответ:6
Объяснение:
Поскольку CD - высота, то угол CDA = 90°.
Рассмотрим получившийся прямоугольный треугольник. Поскольку нам известно, что угол СAD = 30°, то против угла 30° лежит катет, равный половине гипотенузы.
Обозначим его за x. Тогда гипотенуза АС равняется 2 * x.
Воспользуемся теоремой Пифагора:
(2 * x)^2 = x^2 + 18^2;
4 * x^2 - x^2 = 324;
3 * x^2 = 324;
x^2 = 108;
x = √108 = √(9 * 12) = 3 * √12 = 3 * √(4 * 3) = 3 * 2 * √3 = 6 * √3.
AC = 2 * 6 * √3 = 12 * √3
Рассмотрим прямоугольный треугольник АВС. Поскольку нам известно, что угол СAВ = 30°, то против угла 30° лежит катет, равный половине гипотенузы.
Обозначим его за y. Тогда гипотенуза АB равняется 2 * y.
Воспользуемся теоремой Пифагора:
(2 * y)^2 = y^2 + (12 * √3)^2;
4 * y^2 - y^2 = 12^2 * 3;
3 * y^2 = 144 * 3;
y^2 = 144;
y = 12.
AB = 2 * 12 = 24.
Значит:
BD = AB - AD = 24 - 18 = 6 см.
Все обозначения на рисунке.
Углы ABO, CBO равны, т.к. BO - биссектриса, аналогично равны углы BCO и OCA; Дуги AP и PC равны => AP=PC => углы PAC и ACP равны. Угол ABP равен углу ACP, так как они опираются на одну дугу.
1) Выразим через x и y угол PCO: PCO=x+y; Теперь угол POC: POC=180-BOC; BOC=180-x-y => POC=180-(180-x-y)=x+y; Значит PCO=POC что и требовалось.
2) Из доказанного ранее, что не умаляет очевидности этого факта, AP=PC; Так как угол ABC = 120, то угол APC=60; Следовательно треугольник APC является равносторонним. Найдем AC по известной формуле: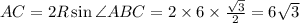
; Площадь треугольника APC: 