Объяснение:
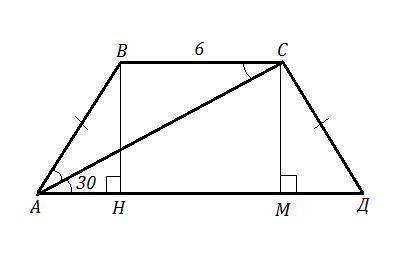
АВСД - равнобокая трапеция, АВ=СД, ВС=6 см, ∠АВС=120° , ∠САД=30°. Найти АС.
Так как ∠АВС=120°, то ∠ВАД=180°-120°=60° ,
∠САД=30° ⇒ ∠ВАС=∠ВАД-∠САД=60°-30°=30° .
Значит диагональ АС - биссектриса ∠А .
∠АСВ=∠САД=30° как внутренние накрест лежащие при АД || ВC и секущей АС ⇒ ΔАВС - равнобедренный , т.к. ∠ВАС=∠АСВ .
Значит, АВ=АС=6 см .
Опустим перпендикуляры на основание АД из вершин В и С: ВН⊥АС , СМ⊥АД , получим прямоугольник ВСМН и два треугольника АВН и СМД .
Рассмотрим ΔАВН: ∠ВНА=90°, ∠ВАН=∠ВАД=60° , АВ=6 см ⇒
∠АВН=90°-80°=30°
Против угла в 30° лежит катет, равный половине гипотенузы ⇒ АН=6:2=3 см.
Так как ΔАВН=ΔСМД (по гипотенузе АВ=СД и острому углу ∠ВАД=∠АДС), то МД=АН=3 см.
НМ=ВС=6 см как противоположные стороны прямоугольника ВСМН.
АД=АН+НМ+МД=3+6+3=12 см.
Объяснение:
АВСД - равнобокая трапеция, АВ=СД, ВС=6 см, ∠АВС=120° , ∠САД=30°. Найти АС.
Так как ∠АВС=120°, то ∠ВАД=180°-120°=60° ,
∠САД=30° ⇒ ∠ВАС=∠ВАД-∠САД=60°-30°=30° .
Значит диагональ АС - биссектриса ∠А .
∠АСВ=∠САД=30° как внутренние накрест лежащие при АД || ВC и секущей АС ⇒ ΔАВС - равнобедренный , т.к. ∠ВАС=∠АСВ .
Значит, АВ=АС=6 см .
Опустим перпендикуляры на основание АД из вершин В и С: ВН⊥АС , СМ⊥АД , получим прямоугольник ВСМН и два треугольника АВН и СМД .
Рассмотрим ΔАВН: ∠ВНА=90°, ∠ВАН=∠ВАД=60° , АВ=6 см ⇒
∠АВН=90°-80°=30°
Против угла в 30° лежит катет, равный половине гипотенузы ⇒ АН=6:2=3 см.
Так как ΔАВН=ΔСМД (по гипотенузе АВ=СД и острому углу ∠ВАД=∠АДС), то МД=АН=3 см.
НМ=ВС=6 см как противоположные стороны прямоугольника ВСМН.
АД=АН+НМ+МД=3+6+3=12 см.

Продлим линию КР до пересечения с плоскостью авс. Пусть точка пересечения O. Сделаем проекцию КР на плоскость авс. Проекция КР пройдет через вершину а и пересечет линию вс в точке, которую назовем D. Точки О, а, D окажутся на одной линии. Найдя угол КОD, мы найдем угол между плоскостью авс и плоскостью в1кр. aD является высотой в равностороннем треугольнике авс. Пусть х - сторона правильной призмы. Вычислим aD. Так как высота в равностороннем треугольнике является и медианой, то вD=1/2х По теореме Пифагора
Рассмотрим треугольник КОD
В нем аР является средней линией, так как аР=1/2аа1=1/2КD
Тогда
Таким образом, угол KOD=30 градусов
ответ: угол между плоскостью авс и плоскостью в1кр равен 30 градусов.