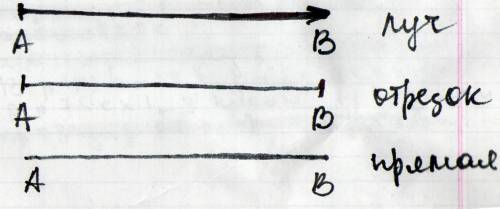
луч может еще быть по другому нарисован (начинается как отрезок, а кончается как прямая
Объяснение:
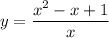
1. ОДЗ: х≠0;
или х ∈ (-∞; 0) ∪ (0; +∞)
2. Четность, нечетность.
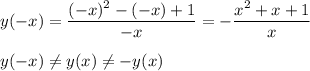
⇒ функция не является четной или нечетной, то есть - общего вида.
3. Пересечение с осями.
1) х ≠ 0 ⇒ ось 0у не пересекает.
2) у = 0 ⇒
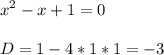
⇒ корней нет, то есть ось 0х не пересекает.
4. Асимптоты.
1) Вертикальная.
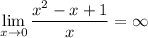
⇒ x=0 - вертикальная асимптота.
2) Наклонная: у = kx + b
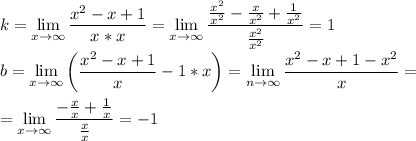
⇒ y = x - 1 - наклонная асимптота.
5. Возрастание, убывание, экстремумы.
Найдем производную, приравняем к 0, найдем корни и отметим их на числовой оси. Определим знаки производной на промежутках. Если "+" - возрастает, если "-" - убывает.
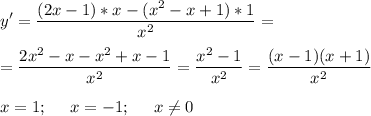
[1]](/tpl/images/4742/2827/17b64.png)
Возрастает при х ∈ (-∞; -1] ∪ [1; +∞)
Убывает при х ∈ [-1; 0) ∪ (0; 1]
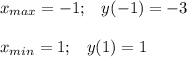
6. Выпуклость, вогнутость.
Найдем производную второго порядка.
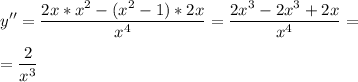
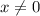
Найдем знак второй производной на промежутках. Если "+" - вогнута, если "-" - выпукла.
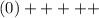
Выпуклая при х ∈ (-∞; 0)
Вогнутая при х ∈ (0; +∞)
Строим график.
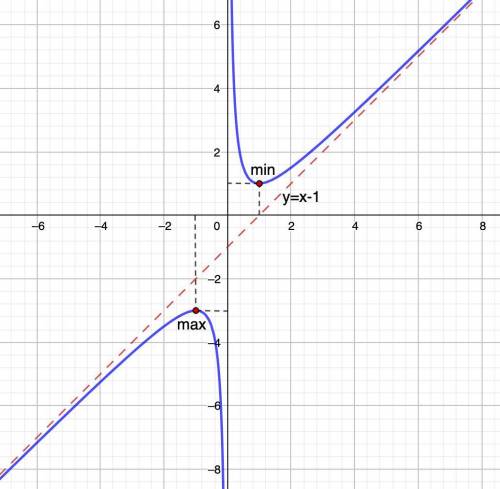
Луч АВ начинается в т.А и через т.В идет дальше( ограничен только со стороны т.А)
Прямая АВ- проходит через А и В, но бесконечна(дальше А и В идет)
АВ луч
АВ прямая
АВ отрезок (ограничен А и В)