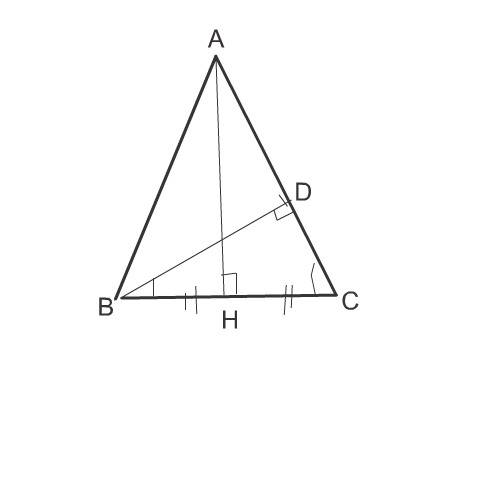
Треугольник АВС с основанием ВС - равнобедренный.
Из вершины А этого треугольника опустим высоту АН на основание ВС
Т.к. треугольник равобедренный, эта высота, являясь и медианой, делит основание ВС на две равные части.
Рассмотрим треугольники АНС и ВDС.
Они подобны, так как угол С в них общий, а прямоугольные треугольники с равным острым углом подобны.
ВD:АН=DC:НС
Из прямоугольного треугольника ВDС найдем катет DC по теоеме Пифагора
СD²=ВС²- DB²
СD²=900-576=324
СD=18
ВD:АН=DC:НС
24:АН=18:15
18 АН=360
АН=20
Площадь АВС=АН*НС
S АВС=20*15=300 см²
Площадь круга пR^2 = 961п Отсюда R= корень из 961, т.е. 31
Трапеция ABCD AD - большее основание. Из т.В и С опускаем перпендикуляр на AD. Получаются точки E,F. В треугольнике ABE угол А=60, отсюда угол В=30. АЕ лежит напротив угла 30, значит она 1/2 гипотенузы АВ, т.е. 8/2=4. FD тоже 4. ВЕ равен 8*cos30= 8*(корень из 3)/2, или 4*(корень из 3).
Верхнее основание х, нижнее х+8, высота4*(корень из 3). Площадь трапеции равна
((х+8)+х)*4(корень из 3)/2 = 68*(корень из 3) (2х+8) =34 x=13. Большее основание = 13+4+4 = 21
а) из треугольника ABOBO = H / tn(бета)б) из треугольника COD - проэкция искомой плоскости на основу конуса:BC = BO * tn(альфа/2) = H / tn(бета) * tn(альфа/2)а площадь треугольника COD = BO * BC = H / tn(бета) * H / tn(бета) * tn(альфа/2) = H^2 * tn(альфа/2) / tn^2(бета)учитывая что мы нашли площадь проэкции, искомая площадь = S_проэкции / cos (бета)S_треуг(ACD) = S(COD) / cos (бета) = H^2 * tn(альфа/2) / tn^2(бета) / cos (бета) = H^2 * tn(альфа/2) * cos (бета) / sin^2(бета)
2.перпендикуляр делит треугольник ABO на 2 треугольника BOH и OAH.все 3 треугольника подобны друг другу, поэтому можно составить пропорции:AH / OH = OH / BH36 / OH = OH / 64OH ^ 2 =36 * 64OH = корень (36 * 64) = 6 * 8 = 48воспользовавшись теоремой пифагора для треугольника BOH найдём гипотенузу:BO = корень(OH ^ 2 + BH ^ 2) = корень (48 ^ 2 + 64 ^ 2)= корень (16*16 * 3*3 + 16*16 * 4*4) = = 16 * корень(25) = 16*5 = 80