1)Сумма внешних углов не зависит от n и равна 2π. Следовательно внешний угол правильного девятиугольника равен 360°:9=40°
2)формула суммы внутренних углов выпуклого мн-ка 180*(н-2), где н число сторон
решается уравнение: 2520=180(н-2) 18н-36 =252 18н=252+36 н=(252+36):18
3)Раз все углы одинаковы - то и все стороны одинаковы, значит многоугольник правильный.
Угол правильного мн-ника рассчитывается по интересной формуле Alpha = (180*n - 360) / n = 180 - 360 / n Здесь n - это количество сторон, которое нам надо узнать 135 = 180 - 360/n 360/n = 180 - 135 = 45 n = 360/45 = 8
4)
пусть (х) см приходится на 1 часть, тогда (7х) см-1 сторона (меньшая) (8х) см-2 сторона (9х) см-3сторона (10х) см-4 сторона. Зная, что периметр равен 68 см, составим и решим уравнение: 7х+8х+9х+10х=6834х=68х=22см проходится на 1 часть2*7=14(см) -меньшая сторонаответ: 14сиответ: 14 см
3)7*2=14 см - меньшая сторона
5)УсловиеВ выпуклом четырехугольнике ABCD отрезок, соединяющий середины сторон AB и CD равен 1. Прямые BC и AD перпендикулярны. Найдите отрезок, соединяющий середины диагоналей AC и BD. Скрыть с вершинами в серединах AB, AC, CB и BD - прямоугольник. РешениеПусть K и M - середины сторон соответственно AB и CD четырехугольника ABCD, а N и L - середины его диагоналей соответственно AC и BD. Тогда KLMN - параллелограмм, а т. к. KN || BC, KL || AD и BC AD, то он - прямоугольник. Следовательно, NL = KM = 1. ответ1.
6)В выпуклом многоугольнике сумма дополнений углов до развернутого равна 360°. В данном случае для первых пяти углов она равна 40 * 5 = 200°. Остается 160°. Это число нельзя представить даже в виде двух слагаемых, каждое из которых > 90° (если остальные углы острые, то дополнительные >90°). Поэтому к пяти имеющимся углам можно добавить только один. а данный многоугольник - шестиугольник
Объяснение:
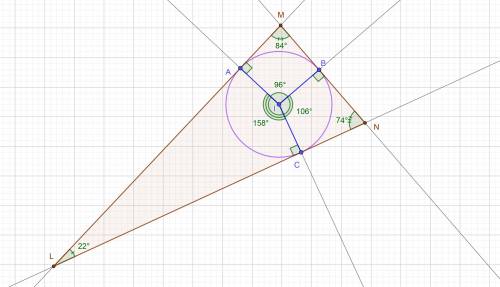
Дуга равна соответственному центральному углу.
∪CA = 360°−∪AB−∪BC = 360−96−106 = 158°
I — центр вписанной окружности в треугольник; IA = IB = IC — радиусы.
∢AIC = ∪CA = 158°; ∢AIB = ∪AB = 96°; ∢BIC = ∪BC = 106°
IA ⊥ LM, IB ⊥ MN, IC ⊥ NL (радиус ⊥ к касательной)
∢IAM = ∢MBI = ∢IBN = ∢NCI = ∢ICL = ∢LAI = 90°
∢L= 360°−∢AIC−∢LAI−∢ICL = 360−158−90−90 = 360−180−158 =180(2-1)-158=180-158 = 22° (из 4-угольника AICL)
аналогично для других углов:
∢ M= 180−96 = 84°
∢ N= 180−106 = 74°
∢L= 22°∢M = 84°∢N = 74°∪CA = 158°