Сечение цилиндра, проведенное параллельно его оси, находится на расстоянии 2 см от нее и является квадратом. Площадь боковой поверхности цилиндра равна 8√3π см2 . Найдите площадь сечения.
Объяснение:
S( бок цилиндра)=2πrh, где , r — радиус основания цилиндра, h — высота цилиндра. Тогда 8√3π=2πrh или 4√3=rh . Возведем обе части в квадрат( зачем? пригодится) (4√3)²=r²h ² , 48=r²h² (*) .
В сечении -квадрат АВСК. Причем АВ=BC=h. Площадь сечения S(квадрата)=BC²=h².Используя (*) h²=S=48:r² .
Т.к. сечение цилиндра, проведенное параллельно его оси, находится на расстоянии 2 см , то ОМ⊥ВС , ОМ=2 см.
ΔВСО-равнобедренный и ОМ-высота , а значит медиана . Тогда
ВМ=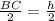
.
ΔВМО-прямоугольный по т. Пифагора r²=2²+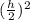
или
r²=4+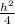 
или r²=
.
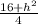S=48 : =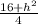 
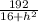(см²)
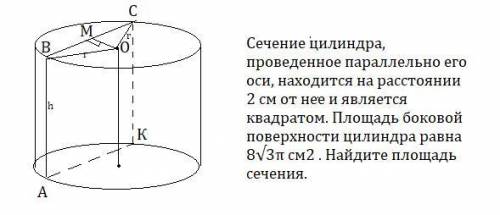
=> <BМD=90°(т.к DМ-высота)
<BDМ=19°(т.к DМ-биссектриса и делит угол ВDC пополам 38/2=19)