углы BОD и СОЕ равны
Объяснение:
Мы можем видеть, что у углов АОЕ и ВОF имеется общая часть, угол ВОЕ.
Так как из условия "Углы АОЕ и ВОF на рисунке 45 равны", и мы вычтем из углов их общую чать, то получим, что угол ЕОF равен углу ВОА.
А так как ОВ и OE — биссектрисы углов АОС и DOF, то можем сделать вывод, что угол DOЕ равен углу СОВ.
Углы BОD и СОЕ можно представить как сумму общей для углов части, угол DOС с соответствующими углами СОВ и DOЕ. И так как угол DOЕ равен углу СОВ, следует, что углы BОD и СОЕ равны.
Объяснение:
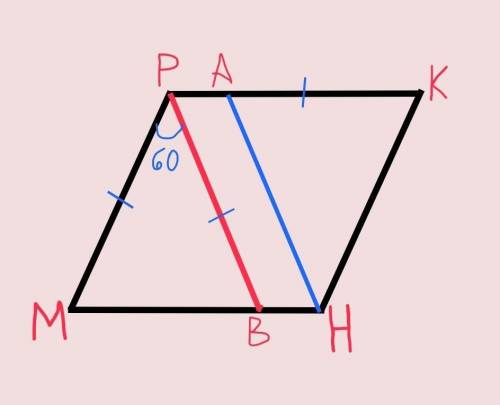
Так как МР=РВ по условию, то ∆МРВ – равнобедренный. Углы при основании равнобедренного треугольника равны, а сумма всех углов равна 180°.
Тогда угол PMB=угол РВМ=(180°–МРВ)÷2=(180°–60°)÷2=60°.
Получим что все углы ∆МРВ равны 60°, тогда ∆МРВ – равносторонний.
Тогда МВ=МР.
Углы при одной стороне параллелограмма в сумме равны 180°.
Значит угол МРК=180°–угол РМВ=180°–60°=120°
Противоположные углы параллелограмма равны.
Следовательно угол РКН=угол РМН=60°; угол МНК=угол МРК=120°.
МР=АК по условию
МР=КН так как противоположные стороны параллелограмма равны.
Углы при основании равнобедренного треугольника равны, а сумма всех углов равна 180°.
Следовательно: угол КАН=угол КНА=(180°–угол АКН)÷2=(180°–60°)÷2=60°.
Получим что все углы ∆АКН равны 60°, тогда ∆АКН – равносторонний. Исходя из этого АН=АК
МВ=МР=АК=АН => МВ=АН.
ответ: 1) 60°; 120; 2) равны.
1. АВ параллельна СД,то уголВСД=углу АВС= 7 градусов( так как они накрест лежащие при параллельных прямых)
2.Если авс равнобедренный,,то угол ВСА=углу АВС=37 градусам, значит угол ВАС=180-37-37=106 градусов