Площадь боковой поверхности пирамиды равна половине произведения апофемы на периметр основания.
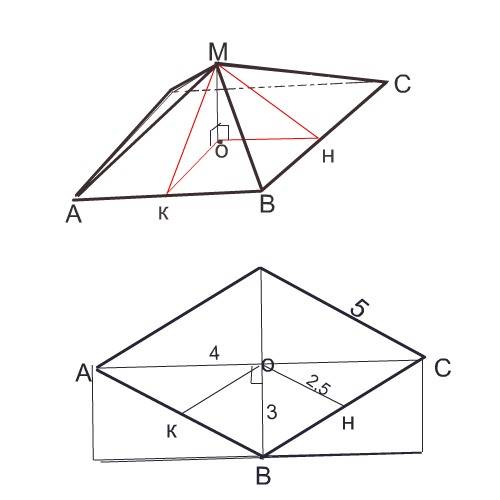
Начертив отдельно основание пирамиды, заметим, что диагонали делят ромб на 4 "египетских" треугольника, отношение сторон в которых равно 3:4:5. Следовательно, сторона ромба равна 5 см.
Площадь каждой грани равна половине произведения апофемы на сторону ромба.
Апофему найдем из треугольника ОМН = ОМК
Если высота пирамиды равна 1 см, то
МН=√(2,5²+1²)=√7,25 см
S бок.=1/2* 4*5√7,25 =10 √7,25 см² или 50√0,29 см²
Медианы треугольника пересекаются в одной точке. Эта точка делит каждую медиану в отношении 2:1 (считая от вершины).
Медианы в правильном треугольнике равны.
R =10см - 2 части - отрезок от точки пересечения медиан до вершины
Вся медиана - 15см
ответ: 15 см
Периметр правильного пятиугольника,вписанного в окружность равен 6дм.найдите сторону правильного треугольника, вписанного в ту же окружность.
Решение: Периметр правильного пятиугольника равен P=5*a, где а –сторона пятиугольника.
Сторона правильного пятиугольника равна a=P\5.
a=6\5=1.2 дм
Радиус описанной окружности правильного пятиугольника:
R=корень(10)\10*корень(5+корень(5))*а, где – а сторона пятиугольника
R= корень(10)\10*корень(5+корень(5))*1.2=
=3\ 25*корень(10)*корень(5+корень(5)) дм
Сторона правильного треугольника равна b=R*корень(3), где R- радиус описанной окружности правильного треугольника (при условиях задачи радиус описанной окружности правильного пятиугольника= радиус описанной окружности правильного треугольника)
b= 3\ 25*корень(10)*корень(5+корень(5))*корень(3)=
3\ 25*корень(30)*корень(5+корень(5)) дм
ответ: 3\ 25*корень(30)*корень(5+корень(5)) дм