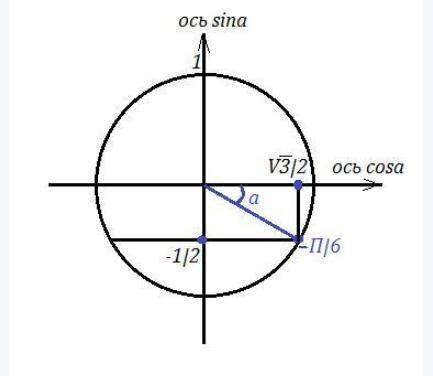
1. а)Уравнение окружности х²+у²=1 этой окружности принадлежит точка В(√3/2;-1/2), т.к. подставляя в уравнение окружности, получим
3/4+1/4=1. остальные не подходят.
б) Эта точка лежит в четвертой четверти, ей соответствует угол 330°, или в радианной мере 11π/6; косинус этого угла равен абсциссе точки, т.е. √3/2, синус - ее ординате, т.е. -1/2, тангенс - отношение синуса к косинусу, т.е. -1/√3=-√3/3, а котангенс обратен тангенсу, и равен -√3. Проверим, например синус sin330°=sin(360°-30°)=sin30°=-1/2
cos330°=cos(360°-30°)=cos(-30°)=cos30°=√3/2
2. по теореме косинусов х²=а²+b²-2ab*cosα; третья сторона х=√(25+16-2*4*5*0.5)=√21/см/; периметр равен 4+5+√21=(9+√21)/см/
Площадь найдем по формуле s=(a*b*sinα)/2=(4*5*sin60°)/2=20√3/см²/
Радиус окружности, описанной около этого треугольника найдем по следствию из теоремы синусов. а/sinα=2R⇒R=a/(2sinα)=
√21/(2√3/2)=√7/cм/
3. по теореме синусов 12/sin50°=32/sinα⇒sinα=32*sin50°/12=
32*0.766/12≈2/043, решений ноль, т.к. не может синус угла быть больше единицы.
Тебе надо выучить названия углов и их свойства. Если я правильно помню, то например накрест лежащие равны, односторонние в сумме дают 180 градусов и тд. У тебя известны два угла. Тебе надо выяснить, какие они ( накрест лежащие, односторонние или соответственные). Дальше тебе нужно найти им пару.
Вот, например ∠4 + ∠6 = 78°, эти углы накрестлежащие, поэтому ∠4 =∠6 = 78°÷2 = 39°
Потом тебе надо найти вертикальные или смежные углуби если таковые есть:∠2 = ∠4, ∠8 = ∠6эти углы вертикальные,
поэтому ∠2 = 39° и ∠8=39°; ∠1 = ∠3 и ∠7 = ∠5, эти углы вертикальные
∠3 = 180° - ∠4 = 141°, ∠5 = 180° - ∠6 = 141°, так как ∠3 и ∠4, ∠5 и ∠6 - смежные
4. ∠1 = ∠3 и ∠7 = ∠5, так как эти углы вертикальные
Объяснение:
1. Каждая сторона треугольника меньше суммы двух других сторон. Пользуясь этой теоремой, пишем неравенства для сторон шестиугольника.
2. Неравенство для второго вопроса -
PK+KL+LM+MN+NR+PR < PA+KA+DK+DL+LB+BM+ME+EN+NC+RC+PF+FR.
3. Неравенство для третьего вопроса -
2*(PK+KL+LM+MN+NR+PR) < PA+KA+DK+DL+LB+BM+ME+EN+NC+RC+PF+FR+(PK+KL+LM+MN+NR+PR).
4. На картинке.
5. Пользуемся ответами от 3 и 4 задания.Сумма периметров треугольников АВС и DEF равна 16 см (7 см+9 см). Я не знаю, там нужно писать единицы измерения или нет.
Вот такое неравенство в итоге получилось -
2*(PK+KL+LM+MN+NR+PR) < 16 см.
6. Логично, что поделить на 2.
Получаем, что -
2*(PK+KL+LM+MN+NR+PR) < 16 см
PK+KL+LM+MN+NR+PR < 8 см.
1) Точка, лежащая на единичной окружности имеет абсциссу, равную косинусу соответствующего угла, а ординату , равную синусу этого угла.
То есть, если точка А лежит на единичной окружности, то её координаты можно записать так: .
.
Основное тригонометрическое тождество имеет вид: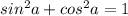 .
.
Поэтому проверяем это тождество для заданных координат.
На единичной окружности лежит точка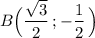 .
.
Найдём значение угла, соответствующего точке В, лежащей на единичной окружности.
Смотри рисунок.
Так как sin любого угла не превосходит 1, то полученный результат говорит о том, что треугольника с такими размерами не существует. Решения задача не имеет .