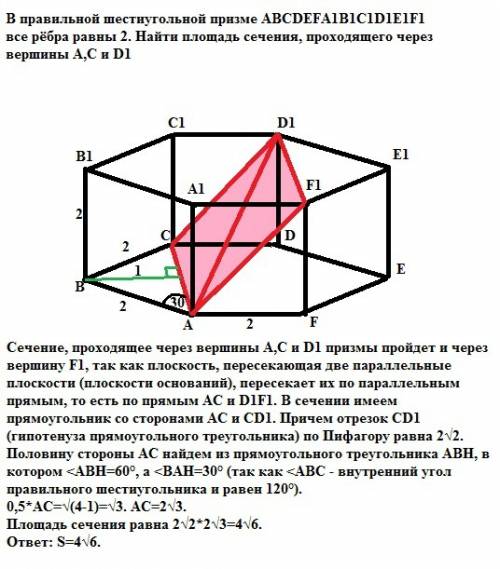
1)
Прямые MK и AD параллельны по условию.
Выясним взаимное расположение прямых MK и AB и угол между ними.
Прямые в пространстве могут пересекаться, быть параллельными или скрещиваться.
Противоположные стороны параллелограмма параллельны, через две параллельные прямые проходит единственная плоскость => все вершины параллелограмма лежат в одной плоскости.
Прямая MK, не лежащая в плоскости ABC, параллельна прямой AD на этой плоскости => MK||(ABC)
=> MK не пересекается с AB.
MK||AD, AD не параллельна AB => MK не параллельна AB.
Таким образом MK и AB скрещиваются.
Угол между скрещивающимися прямыми - угол между параллельными им пересекающимися прямыми.
∠(AB,MK) =∠(AB,AD) =∠BAD =180-130 =50°
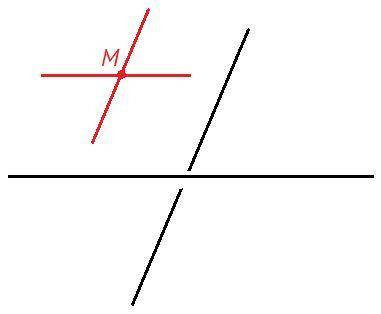
2)
Через точку вне данной прямой можно провести прямую, параллельную данной прямой, и притом только одну.
Через точку M проведем единственные КРАСНЫЕ прямые, параллельные скрещивающимся прямым.
Через две пересекающие прямые проходит плоскость и притом только одна.
Через КРАСНЫЕ прямые проведем единственную КРАСНУЮ плоскость.
Если прямая вне плоскости параллельна прямой в плоскости, то эта прямая параллельна плоскости.
Скрещивающиеся прямые параллельны единственной КРАСНОЙ плоскости.

В1С1/ВС = 3/2
А1С1/АС = 3/2 => треугольник АВС подобен треугольнику А1В1С1 (по трем сторонам)
б) А1В1/АВ = 200/1
В1С1/ВС = 200/1
А1С1/АС = 200/1 => реугольник АВС подобен треугольнику А1В1С1 (по трем сторонам)