У трикутнику MNK кут M=44°,а кут N=56°.Бісектриси NE i MP цього трикутника перетинаються в точці O. Установить відповідність між кутами (1-4) утвореного чотирикутника EOPK і кутами , визначеними умовами (А-Д)
1) кут EOP
2) кут OPK
3)кут PKE
4) кут KEO
A. Більший кут рівнобедреного трикутника , у якого менші кути дорівнюють 50°
Б.Кут суміжний з кутом у 50°
В.Менший кут чотирикутника , у якого три кути рівні між собою , а четвертий на 16° менший за кожен з них
Г. Зовнішній кут рівностороннього трикутника
Д. Найменший кут чотирикутника , кути якого пропорційні числам 4,5,5,6.
Ребята

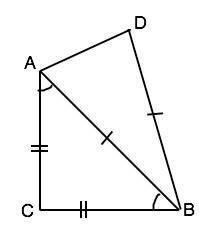
. Дано: ∆ ABC (AC=BC, ∠C=90°) и ∆ ABD– AB=BD. S(ABC)=S(ABD). ∠ADB=?
Решение: Сделаем рисунок, соответствующий условию. Примем АС=СВ=1. Острые углы равнобедренного прямоугольного треугольника равны 45°. Поэтому АB=1:sln45°=√2. Одна из формул площади треугольника S=0,5•a•b•sinα, где a и b стороны треугольника, α - угол между ними. По условию 0,5•АB•CB•sin45°=0,5•AB•BD•sin(∠ABD). BD=AB=√2. Подставив известные величины и сократив равенство на 0,5•АВ•√2, получим 1/2=sin∠ABD Известно, что 1/2= синус 30°. Из суммы углов треугольника ∠BAD+∠ADB=180°-30°=150° ⇒ ∠ADB=∠BAD=150°:2=75°
1) см. рис
А и А1 точки пересечения окружностей с центрами О и К
АР перпендикуляр на продолжение ОК
АР=у
ОР=х
ОА=4
КА=8
ОК=6
х²+у²=4²=16
(х+6)²+у²=8²=64 ⇒ у²=64-(х+6)², подставляем в первое
х²+64-(х+6)²=16
х²+64-х²-12х-36-16=0
12х=12
х=1
у=√(16-1)=√15
l -расстояние от т.О до ц. окр. М касающихся одновременно двух данных, т.е. в т.А и А1 (необходимо найти МА)
МА²=(х+l)²+у²=(1+l)²+15
2)
АВС - треугольник, а=60, В=50, С=70, т.Н пересечение
АА1, ВВ1, СС1 высоты.
<АНС1=<СНА1=<3 (вертикальные)
<BHC1=<CHB1=<1 (вертикальные)
<BHA1=<AHC1=<2 (вертикальные)
ΔВНА1 подобен ΔВСВ1 ⇒<BHA1=<С=70
ΔВНС1 подобен ΔВАВ1 ⇒<BHC1=<А=60
ΔСНА1 полобен ΔСВС1 ⇒<СНА1=<В=50
3) см рис. 2
<α=180-90-48=42°