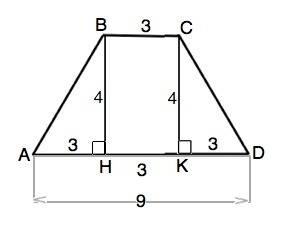
Высотой трапеции называют отрезок прямой, , заключенный между основаниями. и перпендикулярный им. Обычно это отрезок, проведенный из вершины угла при одном основании перпендикулярно к противоположному основанию.
Высота РАВНОБЕДРЕННОЙ трапеции ABCD, проведенная из тупого угла, делит большее основани на отрезки, меньший из которых равен полуразности оснований (на рисунке приложения это АН ( или КD), а больший - их полусумме ( на рисунке это АК или DH).
АН=(АD-ВС):2=3
Из прямоугольного ∆ АВН по т. Пифагора
АВ=√(BH²+AH²)=√(16+9)=5
Трапеция равнобедренная. CD=AB=5
Периметром называется сумма длин всех сторон многоугольника.
P=AB+BC+CD+AD=5+3+5+9=22 см
Если квадрат вписан в окружность значит она для него описанная, тогда мы можем воспользоваться общей формулой РАДИУСА ОПИСАННОЙ ОКРУЖНОСТИ ОКОЛО ПРАВИЛЬНОГО МНОГОУГОЛЬНИКА:
(мы можем ее использовать, т.к. квадрат - правильный четырехугольник)
R = a / (2 sin(360°/2n))
где a - сторона правильного многоугольника n - число сторон многоугольника.
Найдем R = 48 / (2*sin(360/8) = 48/(2*√2/2) = 48/√2
Опять применим ту же формулу для нахождения стороны ПЯТИУГОЛЬНИКА, выведем её:
a = R(2*sin(360°/2n)
a = 48/√2 * sin (36)
В принципе ответ верный, но единственное что может не понравиться- нераскрытый синус
Есть еще одна формула (для правильного пятиугольника): a = R * √((5-√5)/2)
Из нее: a = 48/(√2*2) * √(5 - √5) = 24 / √2 * √(5 - √5)
Выбирай, что нравится :)