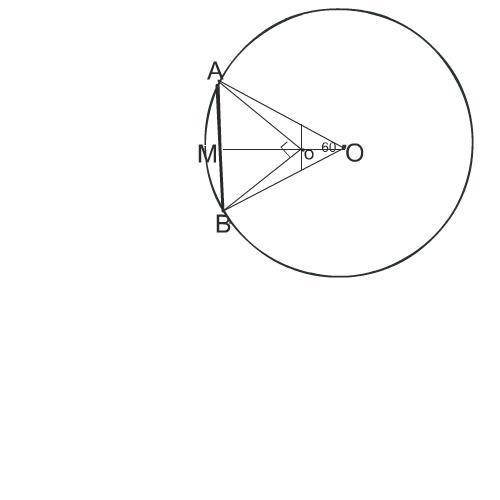
Делаем рисунок к задаче. Не стала рисовать меньшую окружность, чтобы не загромождать рисуно. Ее центр о, радиусы оА и оВ
Так как хорда видна из центра большей окружности под углом 60°,
треугольник АВО - равносторонний.
Хорда АВ равна радиусу ОА.
Проведем высоту ОМ.
Примем сторону АВ=а
ОМ=(а√3):2 по формуле высоты правильного треугольника
Рассмотрим прямоугольный треугольник АоВ
АоВ - равнобедренный, и поэтому оМ в нём равна половине АВ и равна а:2
Запишем выражением разность между ОМ и оМ
(а√3):2 - а:2=(а√3 - а):2=а(√3-1):2
Но это расстояние по условию задачи равно 9(√3-1)
а(√3-1):2=9(√3-1)
Сократим обе части уравнения на (√3-1)
а:2=9
а=9*2=18
Хорда =18
Объяснение:
Назовем отрезок АВ. Точки С и Д (что бы получить три равные части)лежат на отрезке АВ и АС=СД=ДВ
Отрезок длиной 108 м разделен на три равных части, следовательно длина каждой части составляет 108/3=36 см - АС=СД=ДВ=36 см.
Разделим отрезок АС пополам, ставим точку К. И разделим отрезок ДВ пополам ставим точку Р. Расстояние КР нам и надо найти. Это расстояние состоит из:
КС+СД+ДР=КР
Так как АК=КС=36/2=18 см, и ДР=РВ=36/2=18 см, а СД=36 см, то
18+18+36=72 см.
ответ: расстояние между серединами крайних частей (отрезок КР) равно 72 см.