Відповідь:объем параллелепипеда 18; S призмы=62
Пояснення:
Мы помним, что объем параллелепипеда равен Sосн. h. А объем пирамиды равен 1\3*Sосн.* h. Иными словами, если у параллелепипеда и пирамиды одинаковые основания и одинаковые высоты, то объем пирамиды будет в три раза меньше, чем объем параллелепипеда. А у нашей пирамиды еще и площадь основания в два раза меньше. Значит, ее объем в шесть раз меньше объема параллелепипеда.
объем параллелепипеда.=6*обєм пирамиды =6*3=18
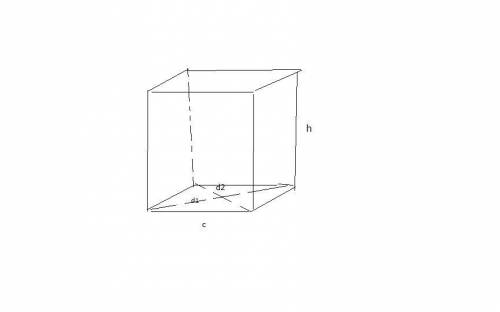
2)площадь основания = 1/2(а*в) где а и в-диагонали
площадь основания = 1/2(3*4)=6
сторону ромба можно найти по формуле С^2 = (d1^2+d2^2)4= (3^2+4^2)4=6.25 c(сторона ромба)=2,5
S боковая = 4(с*h)=4(5*2.5)=50
SПризмы = Sбоковая +2Sосн.=50+6+6=62
1) Так как CL - биссектриса прямого угла С, то
∠ACL = ∠LCB = 90° : 2 = 45°;
2) ∠MCB = ∠LCB - ∠LCM = 45° - 15° = 30°
3) Используем свойство : медиана CM, опущенная на гипотенузу прямоугольного треугольника AB, равна половине гипотенузы.
АМ = МВ = СМ.
4) ΔСМВ - равнобедренный, так как СМ=МВ, значит углы при основании равнобедренного треугольника тоже равны:
∠СМВ = ∠МВС = 30°.
5) ∠САВ = 90° - 30° = 60°;
6) ΔАНС - прямоугольный (с прямым углом Н), так как СН - высота.
∠АСН = 90- 60=30°.
7) ∠LCH = ∠ACL - ∠ACH = 45° - 30° = 15°/
ответ: величина угла LCH = 15°.
96
Объяснение:
Ну, что же ты так? Здесь ведь прямая формула, даже ничего выдумывать не надо: подставляй и получай ответ:
Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро: S(бок.пов.)=P(сеч)*L.
Всё дано (расстояния между боковыми рёбрами и есть перпендикулярное сечение): (3+4+5)*8=12*8=96 см^2.