ответ: катеты 6√5 см и 12√5 см, гипотенуза 30 см. Синусы острых углов 1/√5 и 2/√5
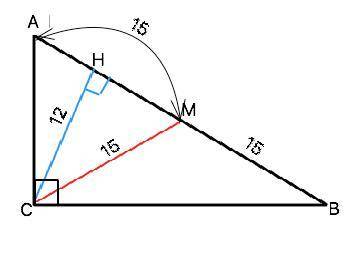
Объяснение: Сделаем согласно условию рисунок и обозначим вершины треугольника АВС ( угол С=90°).
СН=12 см - высота. СМ - медиана. По свойству медианы прямоугольного треугольника из прямого угла АМ=ВМ=СМ=15 см. =>
АВ=2•15=30 см
Из прямоугольного ∆ СНМ катет НМ равен 9 ( египетский). Тогда АН=АМ-МН=15-9=6 ⇒
из ∆ АНС по т. Пифагора АС= √(CH²+AH²)=√180=6√5
из ∆ ВНС по т. Пифагора ВС=√(CН²+BH²)=√720=12√5
Синус угла равен отношению противолежащего ему катета к гипотенузе.
sin ∠CAB=AC:AB=(6√5):30=1/√5 или ≈0,4472
sin ∠CBA=BC:AB=(12√5):30=2/√5 или ≈0,8944
120см
Объяснение:
Дано: ВС = 40см; АЕ - биссектриса угла А; ВЕ = ЕС
Найти: периметр P прямоугольника АВСD
Биссектиса АЕ делит угол А прямоугольника АВСD пополам т.е.
∠BAЕ = 45°.
Поскольку ΔАВЕ прямоугольный (∠В = 90°), то оставшийся угол
∠ВЕА этого треугольника равен ∠ВЕА = ∠В - ∠ВАЕ = 90° - 45° = 45°.
Следовательно, ΔАВЕ равнобедренный, и АВ = ВЕ.
А поскольку ВЕ = 0,5ВС = 0,5 · 40 = 20(см), то и меньшая сторона АВ прямоугольника АВСD равна 20см.
Тогда периметр прямоугольника Р = 2 · (АВ + ВС) = 2 · (20 + 40) = 120(см)

Все грани правильной пирамиды - равнобедренные треугольники.
Поэтому если плоский угол ври вершине равен 60°, то эти треугольники - равносторонние. Следовательно, стороны основания равны боковому ребру.
Поэтому в пирамиде МАВС
АВ=ВС=АС= МА=4 см.
Объём пирамиды равен одной трети произведения её высоты на площадь основания.
Для правильного треугольника
S(АВС=(a²√3):4
S=16√3/4=4√3
Центр ∆ АВС лежит в точке пересечения медиан (высот, биссектрис) правильного треугольника.
По свойству медиан АО=2/3•АН=АВ•sin60°•2/3
AO=(4•√3/2)•2/3=4/√3
Из прямоугольного ∆ АМО по т.Пифагора
МО=√(АМ²-АО²)=(4√2)/√3
V=
-------
Правильная треугольная пирамида с плоским углом при вершине 60° - правильный тетраэдр.
Формула его объёма