32,475 ед²
Объяснение:
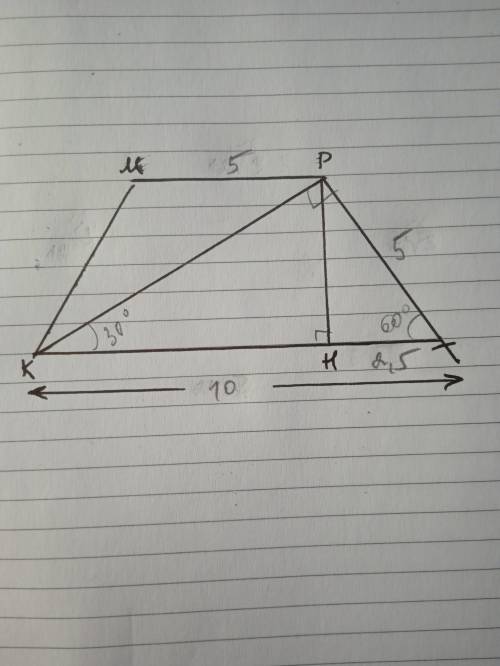
Дано: КМРТ - трапеция, КМ=РТ, КТ=10; ∠К=∠Т=60°. КР⊥РТ Найти S(КМРТ).
ΔКРТ - прямоугольный, ∠Т=60°, ∠РКТ=90-60=30°, т.к. сумма острых углов прямоугольного треугольника 90°
РТ=1\2 КТ=10:2=5 по свойству катета, лежащего против угла 30°
Проведем высоты МС и РН, рассмотрим ΔТРН - прямоугольный,
∠ТРН=90-60=30°, значит ТН=1/2 РТ=5:2=2,5.
По теореме Пифагора РН=√(РТ²-ТН²)=√(25-6,25)=√18,75≈4,33
ΔКМС=ΔТРН по катету и гипотенузе, значит КС=ТН=2,5;
МР=СН=10-2,5-2,5=5.
S=(МР+КТ):2*РН=(5+10):2*4,33≈32,475 ед²
Рассмотрим боковую грань. Это равнобокая трапеция с основаниями 2 и 8, боковые стороны по 6.
Высота этой трапеции - это апофема А пирамиды.
А = √((6² - ((8-2)/2)²) = √(36 - 9) = √27 = 3√3 см.
Теперь проведём осевое сечение пирамиды через боковое ребро.
В сечении - трапеция с основаниями, равными высотам оснований.
У верхнего h = 2(√3/2) = √3 см.
У нижнего h = 8(√3/2) = 4√3 см.
Проекция бокового ребра на основание равна разности (2/3) высот.
Эта величина равна (2/3)*(4√3 - √3) = (2/3)*3√3 = 2√3 см.
Отсюда находим высоту пирамиды.
Н = √(6² - (2√3)²) = √(36 - 12) = √24 = 2√6 см.
угол С=60 / следовательно угол К = 180-60-90=30
угол М=90 /
2) на против угла в 30 градусов лежит катет равный половине гипотенузы, следовательно гипотенуза КС = 2 МС , КС=2*7=14
ответ :14