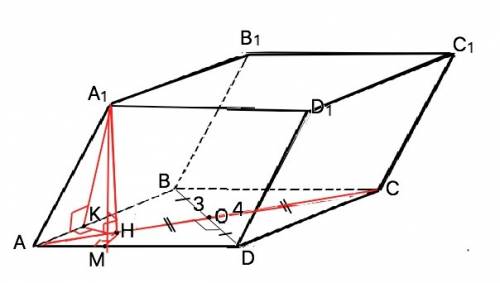
Обозначим вершины параллелепипеда АВСDD1FА1В1С1. Формула объема параллелепипеда V=S•H, где Ѕ - площадь грани, лежащей в основании, Н - высота, т.е. расстояние между параллельными (горизонтальными) гранями.
Ѕ(ромба)=d•d1/2=BD•AC/2=6•8/2=24 см² Диагонали ромба взаимно перпендикулярны и делят его на 4 равных прямоугольных треугольника, катеты которых равны половинам диагоналей. Из соотношения катетов 3:4, эти треугольники – так называемые египетские, ⇒ гипотенузы этих треугольников -стороны ромба– равны 5 см.
По условию все грани параллелепипеда - равные ромбы, ⇒ боковое ребро составляет с соседними сторонами основания равные углы. ∠А1АК=∠А1АМ. Площади равных граней равны, а их высоты – равные перпендикуляры.⇒ А1К=А1М. Из формулы площади параллелограмма h=S:a=24/5 см. По т.Пифагора АК=√(AA1²-A1К²)=√(5²-(24/5)²)=7/5 см.
Треугольники АКА1 и АМА1 равны по катетам и общей гипотенузе АА1 Проекции равных наклонных А1К и А1М равны. ⇒ НК=НМ. Отсюда прямоугольные ∆ АКН=∆ АМН, их острые углы равны. Поэтому основание высоты А1Н параллелепипеда лежит на биссектрисе угла ВАD, т.е. на диагонали ромба. Прямоугольные ∆ АКН ~∆ АВО по общему острому углу при А. Из подобия следует отношение АН:АВ=АК:АО ⇒АН:5=(7/5):4 ⇒ АН=7/4. т.Пифагора А1Н=(√(AA1²-АН*)=√((400-49):4))=√(9•39/16). АН=0,75√39. V(параллелеп)=24• 0,75√39=18√39 или ≈ 112,41 см³
Вычислим высоту трапеции.
Для этого проведём отрезок СМ║AD.
В четырехугольнике АМСD противоположные стороны параллельны, следовательно, ADCM- параллелограмм.
СМ=AD=3, AM=CD=18
В ∆ МСВ стороны СМ=3, СВ=6√2, МВ=АВ - СD=9
Опустим высоту СН. Пусть МН=х, тогда ВН=9-х
Выразим по т.Пифагора из ∆ СНМ квадрат высоты СН
СН²=СМ²-МН²=9-х²
Выразим по т.Пифагора из ∆ СНВ квадрат высоты СН
СН²=СВ²-ВН²=72-81+18х-х²
Приравняем найденные значения СН²
9-х²=72-81+18х-х² откуда 18=18х,⇒ х=1
СН=√(9-1)=√8
Высота ∆ ADC=CH=√8=2√2
S ADC =2√2•18:2=9√8=18√2
По равным накрестлежащим и вертикальным углам ∆CDK~∆ACB с k=18/27=2/3
Высота ∆ ADK и ∆CDK, проведённая из общей вершины D, одна и та же. Площади треугольников с равными высотами относятся как их основания.
Тогда АК:КС=3:2. Т.е. SADK=3/5 S ∆ ADC
S ∆ ADK=3•(18√2):5•3=10,8√2 ед площади

Дано:АВСD-параллелограмм,P=80см,АС=30см
Найти: Р треуг.АВС
B C
1 ) / /
/ /
A / /D
проведем АС бессектриссу
у нас получильсь 2 трегольника
нам известна площадь параллелограмма =80см,значит Р АВС = 40см
Так как переметр параллелограмма= 80см а биссектрисса делит параллелограмм на 2 треугольника АВС и АСD
80:2=40см(периметр АВС)
ответ:РАВС=40см