Правильная четырёхугольная призма.
АВ = 4 см.
AC1 = 4√3 см.
Найти:V - ?
Решение:"Правильный многоугольник - многоугольник, у которого все углы и стороны равны".
Так как данная призма - правильная, четырёхугольная => основание этой призмы - квадрат.
"Квадрат - геометрическая фигура, у которой все стороны равны".
=> АВ = AD = CD = CB = 4 см.
АС - диагональ квадрата.
d = a√2, где d - диагональ квадрата АС; а - сторона квадрата.
=> АС = 4√2 см.
СС1 = h призмы.
Найдём СС1 (h), по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; а, b - катеты)
a = √(c² - b²) = √((4√3)² - (4√2)²) = 4 см.
Итак, СС1 = h = 4 см.
V = S основания * h
Основание - квадрат.
S квадрата = а² = 4² = 16 см.
V = 16 * 4 = 64 см³
ответ: 64 см³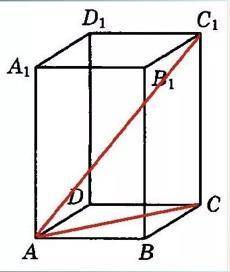
Правильная четырёхугольная призма.
АВ = 4 см.
AC1 = 4√3 см.
Найти:V - ?
Решение:"Правильный многоугольник - многоугольник, у которого все углы и стороны равны".
Так как данная призма - правильная, четырёхугольная => основание этой призмы - квадрат.
"Квадрат - геометрическая фигура, у которой все стороны равны".
=> АВ = AD = CD = CB = 4 см.
АС - диагональ квадрата.
d = a√2, где d - диагональ квадрата АС; а - сторона квадрата.
=> АС = 4√2 см.
СС1 = h призмы.
Найдём СС1 (h), по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; а, b - катеты)
a = √(c² - b²) = √((4√3)² - (4√2)²) = 4 см.
Итак, СС1 = h = 4 см.
V = S основания * h
Основание - квадрат.
S квадрата = а² = 4² = 16 см.
V = 16 * 4 = 64 см³
ответ: 64 см³