Несколько теорем к решению данной задачи :
1. В равнобедренном тр-нике боковые стороны равны;
2. Высота в равнобедренном тр-ке делит основание пополам.
3) Теорема Пифагора.
Дано: АВС - равноб.тр-ник
АВ = ВС = 17см
ВН (высота) = 8см
Найти: АС
ВН делит основание на отрезки АН и НС; АН=НС
Рассмотрим треугольник АВН
АВ -гипотенуза, ВН и АН - катеты.
АВН -прямоугольный тр-ник
По т. Пифагора определим АН
АН = YAB^2 - BH^2
AH = Y 17^2 - 8^2 = Y 289 - 64 = Y225 = 15
AC = 2*15 = 30
ответ: АС = 30 см.
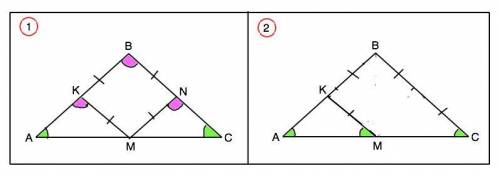
Проведем МN||АВ..
Четырехугольник КВNM - параллелограмм по построению =>
MN=ВК
Рассмотрим треугольники АКМ и СNМ
В равнобедренном треугольнике АВС углы при основании АС равны. =>
∠ВАМ=∠ВСМ
∠АКМ=∠СNМ=∠АВС - соответственные при параллельных прямых и секущей.
Если в треугольниках два угла равны, то равны е третьи углы. => ∠КАМ=∠NMC
ΔАКМ = ΔСNM по второму признаку равенства треугольников. Сходственные элементы равных треугольников равны. =>
АМ=СМ, ч.т.д.
————
Или:
КМ||ВС по условию,, ⇒∠КМА=∠ВСМ - соответственные при параллельных прямых КМ и ВС и секущей АС.
Δ АВС равнобедренный ⇒ ∠ВАС=∠ВСА, следовательно, в ∆ АКМ углы при М и А равны, ∆ АКМ - равнобедренный. КА=КМ=ВК
КМ параллельна ВС ⇒ КМ - средняя линия ∆ АВС и М - середина АС. Отсюда следует равенство АМ=МС.
Можно только сказать что, они будут параллельны, только в том случае, если CO = OD, a AO = OB.