
Объяснение:
10)
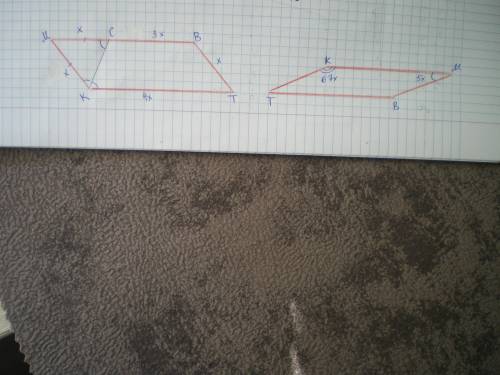
Дано: КМВТ - параллелограмм, Р=65 см, КС - биссектриса, МС/ВС=1/3.
Найти МВ.
∠МКС=∠СКТ по определению биссектрисы
∠СКТ=∠МСК как внутренние накрест лежащие при МВ║КТ и секущей КС
значит, ΔМКС - равнобедренный и МК=МС.
Пусть МС=МК=ВТ=х см, тогда ВС=3х см, КТ=МВ=х+3х=4х см.
Составим уравнение: х+х+4х+4х=65
10х=65; х=6,5
МВ=КТ=6,5 * 4 = 26 см.
ответ: 26 см.
11)
Дано: КМВТ - параллелограмм ∠М/∠К=5/67. Найти ∠К.
Сумма углов параллелограмма, прилегающих к одной стороне, составляет 180°.
Пусть ∠5х°, тогда ∠К=67х°.
Составим уравнение:
5х+67х=180; 72х=180; х=2,5
∠К=67*2,5=167,5°
ответ: 167,5°
параллелепипеде верны следующие равенства:
\begin{gathered}\vec{AB}=\vec{A_1B_1}=\vec{DC}=\vec{D_1C_1}\\\vec{BC}=\vec{B_1C_1}=\vec{AD}=\vec{A_1D_1}\\\vec{AA_1}=\vec{BB_1}=\vec{DD_1}=\vec{CC_1}\\\end{gathered}AB=A1B1=DC=D1C1BC=B1C1=AD=A1D1AA1=BB1=DD1=CC1
следовательно
\begin{gathered}\vec{AB}+\vec{B_1C_1}+\vec{DD_1}+\vec{CD}=\vec{AB}+\vec{BC}+\vec{CD}+\vec{DD_1}=\vec{AD_1}vec{BD_1}-\vec{B_1C_1}=\vec{BD_1}-\vec{BC}=\vec{CD_1}\end{gathered}AB+B1C1+DD1+CD=AB+BC+CD+DD1=AD1BD1−B1C1=BD1−BC=CD1
2.\begin{gathered}\vec{BN}=\vec{BD}+\vec{DN}=\vec d +\frac{1}{2}\vec{DS}=\vec d+\frac{1}{2}(\vec{BS}-\vec{BD})=\\=\vec d+\frac{1}{2}\vec{BS}-\frac{1}{2}\vec d=\frac{1}{2}\vec d+\frac{1}{2}(\frac{1}{2}(\vec{BA}+\vec{BC}))=\frac{1}{2}\vec d + \frac{1}{4}\vec a + \frac{1}{4}\vec c\end{gathered}BN=BD+DN=d+21DS=d+21(BS−BD)==d+21BS−21d=21d+21(