1. Первоначальные сведения по геометрии появились за 4-5 тысячелетий до наших дней в Древнем Египте. В этих краях ежегодные разливы Нила смывали посевы. Поэтому для того чтобы восстанавливать посевы и уточнять размеры налогов, необходимо было размечать поля и выполнять необходимые подсчёты.
2. Древнегреческие учёные переняли у египтян измерения и учёта земель и назвали эти знания геометрией. "Геометрия" - слово, происходящее от греческих слов "reo" - земля, "метрео" - измерять.
3. Евклид, Пифагор, Мухаммад аль-Хорезми, Ахмад Фергани, Абу Райхан Беруни, Абу Али ибн Сина.
4. Памятник Кок Минор напоминает нам форму цилиндра, а на его поверхности фигуры, похожие на круги, овалы и ромбы.
5. Геометрия изучает пространственные структуры и отношения.
Объяснение:
Вроде всё!)
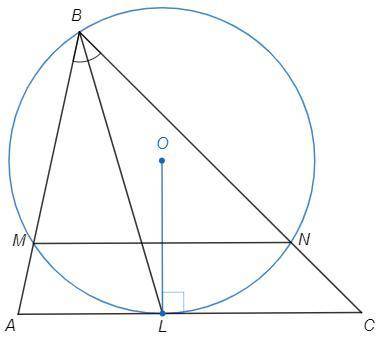
O - центр окружности
OL⊥AC (радиус в точку касания)
Биссектриса BL делит дугу MN пополам.
Радиус OL делит дугу MN пополам, следовательно перпендикулярен хорде MN.
(В равнобедренном △MON биссектриса OL является высотой.)
OL⊥AC, OL⊥MN => MN||AC
По теореме о биссектрисе
AB/AL =BC/CL
По условию
AB +BC =2AC =>
AL*AB/AL +CL*BC/CL =2AC =>
AB/AL (AL+CL) =2AC => AB/AL =2
По теореме о касательной и секущей
AL^2 =AB*AM => AL/AM =AB/AL =2
AL/AM *AB/AL =AB/AM =4/1
△MBN~△ABC (стороны параллельны) => MN/AC =MB/AB =3/4
Объяснение:
Математическая модель задачи:
СЕ - исходное положение "журавля",
АВ - последнее положение.
АК = СК = 2 м - короткое плечо,
ВК = ЕК = 6 м - длинное плечо.
ΔВКЕ подобен ΔАКС по двум пропорциональным сторонам и углу между ними:
ВК : АК = КЕ : КС = 6 : 2 = 3 : 1
углы при вершине К равны как вертикальные.
Из подобия треугольников следует, что
ВЕ : АС = 3 : 1
ВЕ = АС · 3 = 0,8 · 3 = 2,4 м