Объяснение:
Тангенс угла в прямоугольном треугольнике - это отношение противолежащего катета к прилежащему. Проведём дополнительные прямые линии так, чтобы получить прямоугольные треугольники, из которых можно будет найти катеты необходимых углов и воспользуемся формулами тангенса суммы и разности углов.
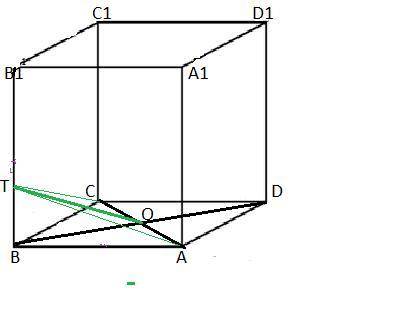
а)
tg∠A = BC / AC = 3/6 = 1/2
ctg∠A = AC / BC = 6/3 = 2
б)
tg∠B = AC / BC = 4/6 = 2/3
ctg∠B = BC / AC = 6/4 = 3/2
№2
Тангенс угла в прямоугольном треугольнике -это отношение противолежащего катета к прилежащему. Проведём дополнительные прямые линии так, чтобы получить прямоугольные треугольники, из которых можно будет найти катеты необходимых углов и воспользуемся формулами тангенса суммы и разности углов.
tg(a-β)=tga-tgβ/1+tga×tgβ; tg(a+β)= tga+tgβ/1-tga×tgβ
a)tg ∠BAC = tg(∠BAD-∠CAD) =tg∠BAD- tg-∠CAD/1+tg∠BAD×tg∠CAD=∠BAD= BK/AK=5/5=1; tg∠CAD= CD/AD=3/6=1/2=1-1/2/1+1×1/2=1/2/3/2=1/3
ctg∠BAD=1/tg∠BAD=1/1/3
b) tg∠ABC=tg(∠CBD+∠KBA) =tg∠CBD+tg∠KBA/1-tg∠CBD×tg∠KBA=tg∠CBD=CD/BD=1/3; tg∠KBA=AK/BK=5/5=1=1/3+1/1-1×1/3=4/3/2/3=4/2=2
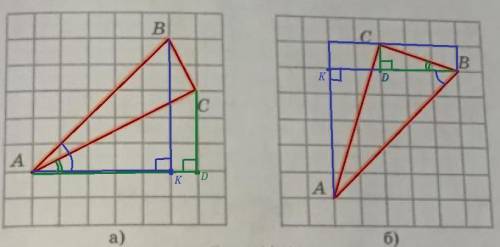
В кубе ABCDA1B1C1D1, ребра которого равны 4, на ребре BB1 взята точка T так, что BT:TB1=1:3. Найти синус угла между плоскостями (АВС) и (АТС)
Объяснение:
Т.к. BT:TB₁=1:3 и ВВ₁=4 ,то ВТ=4:4*1=1 (см).
Из ΔАВС-прямоугольного , по т. Пифагора найдем
АС=√(4²+4²)=4√2 (см). Значит ВD=4√2 см⇒ВО=2√2 см.
В кубе все грани квадраты⇒АС⊥ВD и ТВ⊥ВD ⇒ по т. о трех перпендикулярах ∠ТОВ-линейный угол между плоскостями (АВС) и (АТС).
ΔВТО-прямоугольный , по т. Пифагора ТО²=ВТ²+ТО². ТО=3 см.
sin∠ТВО=ТВ/ТО, sin∠ТВО=1*3.
Синус угла между плоскостями (АВС) и (АТС) равен 1/3.