∆АВС – прямоугольный с прямым углом АВС по условию;
Сумма острых углов в прямоугольном треугольнике равна 90°, тогда угол АСВ=90°–угол ВАС=90°–45°=45°.
Получим что угол ВАС=угол АСВ, следовательно ∆АВС – равнобедренный с основанием АС.
Тогда АВ=ВС=100.
∆ABD – прямоугольный с прямым углом ABD по условию.
Сумма острых углов в прямоугольном треугольнике равна 90°, значит угол ADB=90°–угол BAD=90°–60°=30°.
В прямоугольном треугольнике против угла в 30° лежит катет, вдвое меньший гипотенузы.
Тоесть АВ=0,5*АD => АD=2*АВ=2*100=200.
По теореме Пифагора в прямоугольном ∆АВD:
AD²=AB²+BD²
200²=100²+BD²
40000–10000=BD²
BD=√30000
(BD=–√30000 не может быть, так как длина всегда положительна)
BD=100√3
CD=BD–ВС=100(√3)–100=100((√3)–1)
ответ: 100((√3)–1)
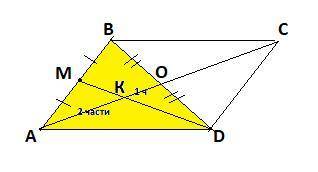
Диагональ АС параллелограмма АBCD равна 18см.Середина М стороны АВ соединена с вершиной D. Найдите отрезки, на которые делится диагональ АС отрезком DM.
Объяснение:
Проведем диагональ ВD, О-точка пересечения диагоналей . По свойству диагоналей параллелограмма АО=ОС=9 см.
Рассмотрим ΔАВD , АО-медиана ( тк. диагонали точкой пересечения делятся пополам) , MD- медиана ( т.к. М-середина по условию).
Пусть К-точка пересечения АО и МD.
По т. о точке пересечения медиан АО:КО=2:1 ⇒АО=9:3*2=6 (см)
Тогда КС=18-6=12 (см)
====================================
Медианы треугольника пересекаются в одной точке и делятся этой точкой на две части в отношении 2:1, считая от вершины.
А=С=57(Равнобедренный треугольник)
Б=180-57-57=66
ответ:Б=66