400=144+Х^2
Х=16
S=16*12=192
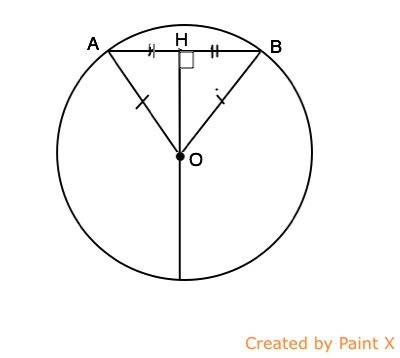
Соединим центр О окружности с концами хорды АВ. ОА=ОВ=R.
Треугольник АОВ - равнобедренный. Проведем высоту ОН этого треугольника.
Угол ОНВ=углу ОНА=90º
«Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один»
Следовательно, и к середине хорды можно провести только один перпендикуляр.
Высота ОН - медиана равнобедренного треугольника.
АН=ВН. Точка Н - середина АВ.
Следовательно, ОН, проходящий через середину АВ, есть срединный перпендикуляр хорды АВ, ч.т.д.
Наверное не диаметр, а диагональ. У прямоугольника нет диаметра.
Тогде решаем так. Диагональ делит прямоугольник на два прямоугольных треугольника. Один из катетов равен 12, а гипотенуза 20. По теореме Пифагора находим вторую сторону: sqrt(400-144)=sqrt(256)=16. Итак стороны прямоугольника 12 и 16, следовательно, площадь равна 12*16=192 кв. см.