Объяснение:
Вычисляем центр диагонали 0А по формуле
: S=(XB+XA)/2 ; (YB+YA)/2
S(OA)=(0+5)/2 ; (5+0)/2 = (5/2;5/2) = (2,5 ; 2,5)
Рассчитаем центр диагонали BО
S(BC)=(1+xB)/2 ; 3+yB)/2
* мы заменяем x и y на x и y z S(OA) (5/2;5/2)
(1+xB)/2=2,5 I *2 ; (3+yB)/2=2,5 I* 2
1+xB=5 3+yB=5
xB=5-1 yB=5-3
xB=4 yB=2
OTBET: Точка поиска B = (4; 2)
(w załączeniu grafik)
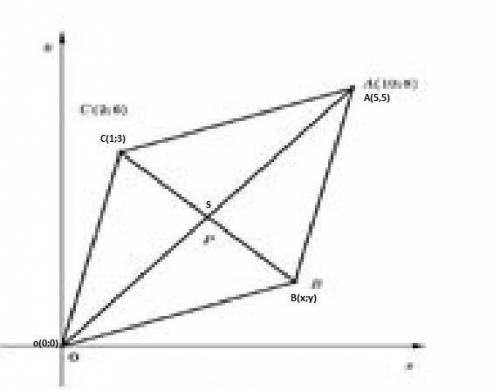
Прикреплена картинка, на ней:
угол CAB обозначим за a
тогда ACB тоже a (равнобедренный треугольник)
угол ABC = 180-a-a = 180-2a (180 сумма углов)
Так как угол ABD развернутый (180 градусов)
то угол CBD, смежный с ABC = 180 - (180-2а) = 2а
т.к. BC = BD(AB=BC по условию, AB = BD по условию), то СBD тоже равнобедренный
и углы BCD и ВDC равны.
т.к. опять же сумма всех углов треугольника BDC = 180,
то оставшихся двух = 180 - СBD = 180-2a.
А одного из них 90-a.
Чтобы найти ACD сложим ACB + BCD = a + 90 - a = 90 градусов,
что и требовалось доказать