1. 8 см
2. 4√3 см
Объяснение:
1. Сторона А(1)А(2) равна радиусу вписанной окружности, то есть двум диаметрам = 2R
В эту окружность вписан правильный треугольник со стороной 4√3 см.
Радиус окружности, описанной около правильного треугольника со стороной а, равен R = a/√3.
Находим радиус: R = 4√3/√3 = 4 см.
Значит, сторона А(1)А(2) равна 2R = 2*4 = 8 см
2. Сторона А(1)А(2) - это сторона правильного шестиугольника, описанного около окружности, в которую вписан правильный треугольник со стороной 6√3 см.
Сначала находим радиус окружности, описанной около этого правильного треугольника, через его сторону. R = a/√3 = 6√3/√3 = 6 см.
Известно, что правильный шестиугольник разбивается на шесть правильных треугольников с высотой, равной радиусу вписанной окружности. Из этого следует, что сторона правильного шестиугольника находится через радиус вписанной окружности по формуле: а = R/sin 60°.
Находим сторону: а = 6:(√3/2) = 6*2 : √3 = 4√3 см
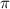 * r, где r - радиус окружности, и равен сумме длин соответствующих 4 дуг. Посему:
* r, где r - радиус окружности, и равен сумме длин соответствующих 4 дуг. Посему: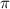 = 2 *
= 2 * 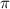 * r
* r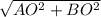 =
= 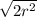 =
= 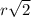 =
= 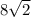 см.
см.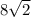 см, AC = BD = 16 см.
см, AC = BD = 16 см.
В прямоугольном треугольнике ADC:
<A=180-<CDA-<DCA=180-90-53=37°
В треугольнике АВС:
<B=180-<C-<A=180-90-37=53°