Площадь равнобедренного треугольника равняется произведению высоты на половину длины основания, то есть
S=ВД*АС/2=5*10√3/2=25√3 см²
ответ: высота ВД=5см, площадь S=25√3 см², углы треугольника равны 30°, 30°, 120°.
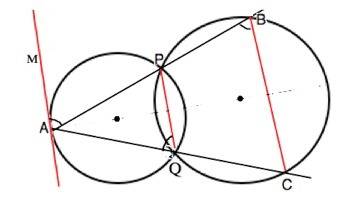
Через т.А проведем касательную АМ
АР- хорда, ∠МАР =дуга АР:2 ( свойство угла между касательной и хордой)
Вписанный ∠АQP=дуга АР:2 ( свойство вписанного угла)⇒
∠МАР=∠АQP.
∠РQC +∠PQA=180°
Во второй окружности сумма противоположных углов вписанного четырехугольника PBCQ равна 180° (свойство), ⇒
∠РQC+<PBC=180° Следовательно, ∠АВС=∠PQA.
Так как ∠PQA=∠PAM, то ∠ABC=∠BAM. Они накрестлежащие, а равенство накрестлежащих углов при пересечении двух прямых секущей – признак параллельных прямых.⇒
МА║ВС , что и требовалось доказать.
S=1/2(AB+CD)*AH (AB и CD-основания трапеции , AH- проведённая высота)
168=1/2(9+19)AH
AH= 12
рассмотрим треугольник DAH-он прямоугольный, т.к. AH-высота
из точки В проведём вторую высоту BL
HL=AB=9
следовательно DH=LC=(19-9)/2=5
в треугольнике DAH по теормеме пифагора DA^2=DH^2+AH^2 (^2-квадрат)
DA=13, DA=BC, т.к. трапеция равнобедренная