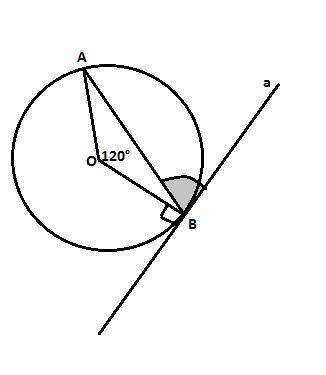
Угол между хордой и касательной равен половине градусной меры дуги, стягиваемой этой хордой (свойство), то есть половине градусной меры дуги АВ.
На дугу АВ опирается центральный угол АОБ, значит дуга АВ = 120°. Значит угол между касательной и хордой в точке касания равен 120°:2 = 60°
ответ: искомый угол равен 60°.
Или так:
В равнобедренном треугольнике АОВ (стороны ОА и ОВ равны - радиусы) углы при основании равны по (180-120):2=30° (сумма углов треугольника = 180°). Касательная в точке касания перпендикулярна радиусу, значит искомый угол равен 90° - 30° = 60°.
ответ: 60°
1)МК(-1-(-2), 3-(-4))=(1,7)
РМ(-2-4,-4-4)=(-6,-8)
2)модуль MK: √(1+7^2)=√50
модуль PM√(6^2+8^2)=10
3)EF(2*1-3*(-6), 2*7-3*(-8))=(20,38), нужно домножить координаты векторов на соответствующие коэффициенты, затем выполнить вычитание соответствующих векторов
4)1*(-6)+7*(-8)=-62, нужно сложить произведения соответствующих координат векторов
5)-62/10√50, т.к Скалярное произведение это произведение модулей векторов и косинуса угла между ними, нужно разделить Скалярное произведение на произведение модулей векторов