ответ:100°;80°;100°;80°;100°;80°;100°;80°;
Объяснение: Пронумеруемо кути
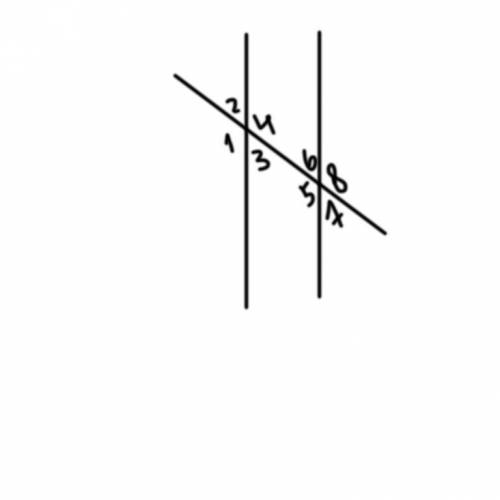
нехай х дорівнює єдиній частині кута, то номер4=5х, а номер6=4х (за вл. внутр. одностор. кутів) маємо рівняння 4х+5х=180°; 9х=180; х=20°; номер4=100°; номер6=80°
номер3=номеру6=80°(за вл. внутр. різностор.)
номер4=номеру5=100°(за вл. внутр. різностор.)
номер4=номеру1=100°(за вл. вертикальних кутів)
номер3=номеру2=80°(за вл. вертикальних кутів)
номер5=номеру8=100°(за вл. вертикальних кутів)
номер6=номеру7=80°(за вл. вертикальних кутів)
Возьмем две точки , лежащие на исходной прямой. Пусть это точка (0;6) и (2;4). Построим точки, симметричные данным относительно точки А(1;-2), для этого учтем А будет серединой отрезка, соединяющего точку (о;6) с ей симметричной точкой (х₁;у₁).
(0+х₁)/2=1, откуда х₁= 2
(6+у₁)/2= -2, откуда у₁=-10, Получили точку (2;-10) симметричную точке (0;6) относительно точки А(1;-2).
Аналогично найдем еще одну искомой прямой. Пусть это будет точка
(х₂;у₂), которая симметрична точке (2;4) относительно А(1;-2)
(2+х₂)/2=1; откуда х₂=0
(4+у₂)/2=-2; откуда у₂=-8
получили еще одну точку (0;-8), симметричную точке (2;4) относительно точки А(1;-2)
Составим теперь уравнение прямой, проходящих через найденные точки (2;-10) и (0;-8)
у = кх +в, подставим в это уравнение прямой сначала одну, потом другую точку, получим систему двух уравнений. ИЗ НЕЕ НАЙДЕМ К И В. И отыщем искомую прямую.
2к+в=-10
0*к+в=-8 из второго уравнения в =-8, тогда из первого 2к=-2, к = -1, искомое уравнение прямой примет вид у = -х-8
ответ у = -х-8
раз вектор АВ равен векторуCD , то соответственно все элементы равны, следовательно начала и концы векторов совпадают. из этого следует, что все точки , лежащие на обоих векторах соответственно совпадают, значит и середины отрезков совпадают. ч.т.д.
обратное
раз середины отрезков, лежащих на АВ и CD совпадают , то все точки этих отрезков совпадают соответственно , а значит и векторы АВ и CD лежат на одной прямой и равны. ч.т.д.