В основании пирамиды лежит квадрат со стороной а, проекция бокового ребра на основания даст половину диагонали квадрата = 12*cos60 = 6 см. Диагональ квадрата
равна 12 см, отсюда сторона квадрата а = 12/√2 см.
Площадь основания a² = 144/2 = 72 см²
Боковая поверхность пирамиды равна площади 4х граней (треугольников) основание которых а, а высота равна апофеме H.
Высота пирамиды находится по боковому ребру h = 12*sin60 = 12*√3/2= 6√3
H=√[(a/2)²+h²] = √[(12/√2)²+(6√3)²] = √(72+12)=√84
s=a*H/2 = 12/√2 * √84/2 = 6√42
Полная поверхность S = 72 + 24√42 ≈ 227,5 см²
В основании пирамиды лежит квадрат со стороной а, проекция бокового ребра на основания даст половину диагонали квадрата = 12*cos60 = 6 см. Диагональ квадрата
равна 12 см, отсюда сторона квадрата а = 12/√2 см.
Площадь основания a² = 144/2 = 72 см²
Боковая поверхность пирамиды равна площади 4х граней (треугольников) основание которых а, а высота равна апофеме H.
Высота пирамиды находится по боковому ребру h = 12*sin60 = 12*√3/2= 6√3
H=√[(a/2)²+h²] = √[(12/√2)²+(6√3)²] = √(72+12)=√84
s=a*H/2 = 12/√2 * √84/2 = 6√42
Полная поверхность S = 72 + 24√42 ≈ 227,5 см²
Расстояние от точки до плоскости равно длине отрезка, проведенного перпендикулярно от точки к плоскости.
Обозначим треугольник АВС, искомое расстояние МО,
Так как расстояния от М до вершин треугольника равны, т.О - центр треугольника АВС и центр описанной около него окружности, в которой АО - радиус.
Формула радиуса описанной окружности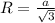 ⇒
⇒
R=3/√3=√3
АO=√3
∆ АМО - прямоугольный.
По т.Пифагора
МО=√(AM²-AO²)=√(4-3)=1 - это ответ.