Основания равнобокой трапеции равны 8 см и 18 см. Точка удалена от каждой стороны трапеции на 10 см. Найдите расстояние от этой точки до плоскости трапеции.
———————
ответ: 8 см.
Объяснение:
Назовем данную точку Е.
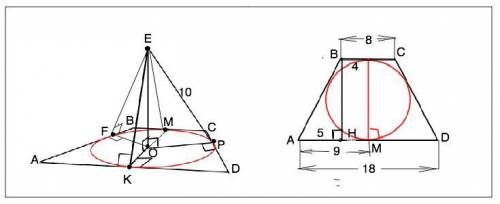
Точка удалена от каждой стороны трапеции на равное расстояние, т.е. на длину перпендикуляров, проведенных от этой точки к сторонам трапеции (см. рисунок во вложении.)
ЕК=ЕF=EM=EP.
Искомое расстояние - перпендикуляр ЕО к плоскости трапеции. Прямоугольные треугольники ЕOF=EOM=EОP=EOK, проекции их гипотенуз - по т. о 3-х перпендикулярах - перпендикулярны сторонам трапеции и равны радиусу вписанной в трапецию окружности.
Суммы противоположных сторон четырехугольника, в который вписана окружность, равны. ⇒ АВ+СD=BC+AD=8+18=26. Боковые стороны равны между собой (дано), ⇒ их длина 26:2=13 см.
Из вершины В трапеции опустим перпендикуляр ВН на АD. Он является высотой трапеции и равен диаметру вписанной окружности.
АН - полуразность оснований. АН=(АD-ВС):2=5.
Из ∆ АВН по т.Пифагора ВН=√(AB²-AH²)=√(13²-5²)=12 см ⇒ d= МК=12, ОК=r=12:2=6 см.
Из ∆ ЕОК по т.Пифагора ЕО=√(EK²-КО²)=√(10²-6²)=8 (см).
сфера вписана в конус.
осевое сечение конуса -равнобедренный треугольник и вписанная окружность.
R=S/p
р=(a+b+c)/2
SΔ=√(p(p-a)(p-b)(p-c))
прямоугольный треугольник:
катет - радиус r основания конуса, найти
гипотенуза - образующая L конуса
катет - высота конуса Н
<α - угол между образующей и радиусом основания
cosα=r/L, r=L*cosα
равнобедренный треугольник со сторонами: L, L, 2r
pΔ=(L+L+2r)/2, pΔ=L+r, pΔ=L+L*cosα, pΔ=L(1+cosα)
SΔ=√((L+r)(L+r-r)(L+r-L)(L+r-L))=√((L+r)*r² *L
SΔ=r*√(L+r)L,
SΔ= (L*cosα)*√L(1+cosα)*L,
SΔ=L*cosα*L*√(1+cosα),
SΔ=L²cosα√(1+cosα)
R= [ L²cosα√(1+cosα) ] / [ L(1+cosα) ]
R=L*cosα√(1+cosα)
Sсферы=4πR
Sсферы=4πLcosα√(1+cosα)
Объяснение:
16:х=4:3
4х=48
х=12