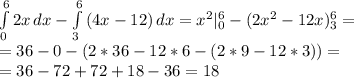

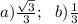
Объяснение:
Смотри прикреплённый рисунок.
Пусть а = 8 см - ребро тетраэдра
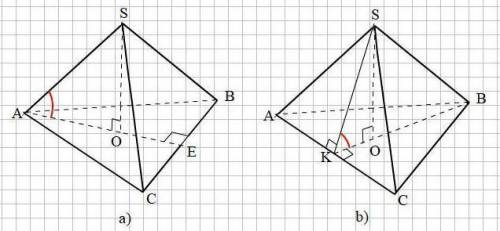
a) В основании АВС проведём высоту АЕ ⊥ ВС. АЕ = 0,5а√3;
Опустим высоту SO на плоскость АВС.
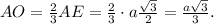
Угол между прямой SA и плоскостью АВС есть угол SAO
b) В основании АВС проведём высоту BK ⊥ AС. BK = 0,5а√3;
Опустим высоту SO на плоскость АВС.
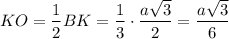
Проведём в грани SAC апофему SK = 0,5а√3
Угол между плоскостями SAC и АВС есть угол SKO между апофемой SK и высотой основания ВК как угол между двумя перпендикулярами, восставленными из точки К к линии пересечения АС плоскостей SAC и АВС
Поскольку тетраэдр правильный, то углы между любой боковой плоскостью и плоскостью основания равны между собой. И косинус между плоскостью SBC и плоскостью АВС равен 1/3.
Рассмотрим треугольники MKA и CKD:
Углы MKA и CKD равны, так как они вертикальные.
Углы КМА и СDK равны, как накрест лежащие углы для параллельных прямых CD и AB и секущей MD.
Углы MAK и KCD равны, как накрест лежащие для параллельных прямых CD и AB и секущей AC
Получается, что треугольники MKA и CKD подобны по трём углам.
То есть AM/CD=AK/КС
Коэффициент подобия равен 1/2, так как 2АМ=DC.
Следовательно, AK/KC=1/2, отсюда 2АК=КС.
АС=КС+АК=2АК+АК=3АК
3АК=18
АК=6, КС=12