Объяснение:
Задача 1:
Так как сумма углов прилежащих к одной стороне равна 180 градусов, значит углы данные в задаче- противолежащие. Противолежащие углы у параллелограмма равны, следовательно:
A + C= 62 равно 2A=62
Пусть A=x, тогда
2x=62
x=31 градус = угол А и следовательно=уголу C (противолежащие углы парал. равны)
Сумма прилежащих к одной стороне углов равна 180 градусов, следовательно, угол B= 180-A=180-31=149 градусов
ответ: угол B=149 градусов
Задача 2:
Так как противолежащие углы параллелограмма равны, а сумма углов прилежащих к одной стороне равна 180, то можно составить уравнение
Пусть угол A - x. Тогда угол D=x+70
x+(x+70)=180
2x+70=180
2x=110
x= 55- градусов угол A
1) D=180 - A= 180-55=125 градусов
ответ: 125 градусов = угол D
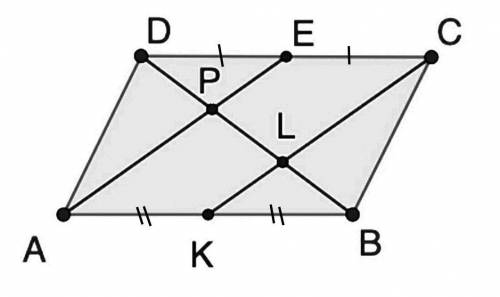
АВ=CD так как противоположные стороны параллелограмма равны. Тогда 0,5*АВ=0,5*CD.
Так как К – середина АВ, то АК=0,5*АВ.
Так как Е – середина CD, то ЕС=0,5*CD.
Получим что АК=ЕС.
АК//ЕС, так как AB//CD, поскольку противоположные стороны параллелограмма параллельны.
Тогда получим что AECK – параллелограмм, так как противоположные стороны паралельны и равны. Следовательно АЕ//КС так как противоположные стороны параллелограмма параллельны.
По обобщённой теореме Фалеса: параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
То есть
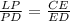
Пусть СЕ=n, тогда ED=n так же, так как CE=ED. Тогда:
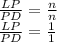
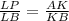
Пусть AK=m, тогда КВ=m так же, так как AK=KB.
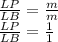
Получим что PD:LP:BL=1:1:1, или иначе говоря отрезки равны.
ответ: 1
т.к косинус, это отношение прилежащего катета на гипотенузу получаем, 8/AB=√3/2, отсюда AB=16√3/2.
по т.Пифагора найдем СВ=8√3
Если синус угла а=0,5 то косинус в=0,5
т.к СН-высота, то тре.СНВ тоже прямоугольный.
т.к кос В=0,5, найдем ВН=8√3/2=4√3
и по т.Пифагора находим СН=√(8√3)^2-(4√3)^2=√144=12
ответ: СН=12