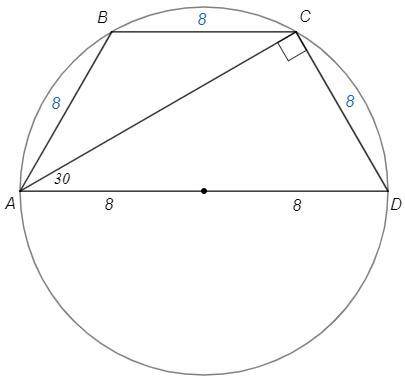
Вписанный прямой угол опирается на диаметр.
ACD=90 => AD=8*2 =16 (диаметр)
Катет против угла 30 равен половине гипотенузы.
CAD=30 => CD=AD/2 =8
Равнобедренная трапеция, боковые стороны равны.
AB=CD =8
Сумма острых углов прямоугольного треугольника 90.
CDA=90-CAD =60
Равнобедренная трапеция, углы при основании равны.
BAD=CDA =60
BAC=BAD-CAD =60-30=30
Вписанный угол равен половине дуги, на которую опирается.
BAC=CAD => ∪BC=∪CD
Равные дуги опираются на равные хорды.
∪BC=∪CD => BC=CD =8
P(ABCD)=8+8+8+16 =40 (см)
Дано:
ABCD — параллелограмм,
AC и BD -диагонали,
AC=BD.
Доказать: ABCD — прямоугольник.
Доказательство:
1. Рассмотрим треугольники ABD и DCA (не забываем, что важно правильно назвать треугольники!).
1) AC=BD (по условию).
2) Сторона AD — общая.
3) AB=CD (как противолежащие стороны параллелограмма).
Следовательно, треугольники ABD и DCA равны (по трем сторонам).
2. Из равенства треугольников следует равенство соответствующих углов:
∠BAD=∠CDA.
3. ∠BAD+∠CDA=180º.(как внутренние накрест лежащие углы при AB ∥ CD и секущей AD).
Пусть ∠BAD=∠CDA=xº, тогда
x+x=180
2x=180
x=90
4. Значит, ∠BAD=∠CDA=90º. Следовательно, ABCD — параллелограмм, у которого есть прямой угол. Отсюда, ABCD — прямоугольник ( по второму признаку прямоугольника).
Что и требовалось доказать.
a = R*√3, тогда R = a / √3 = 12 / √3.
Площадь круга S = πR² = π*(144/3) = π*48 = 3,14159*48 = 150,796 кв.ед.