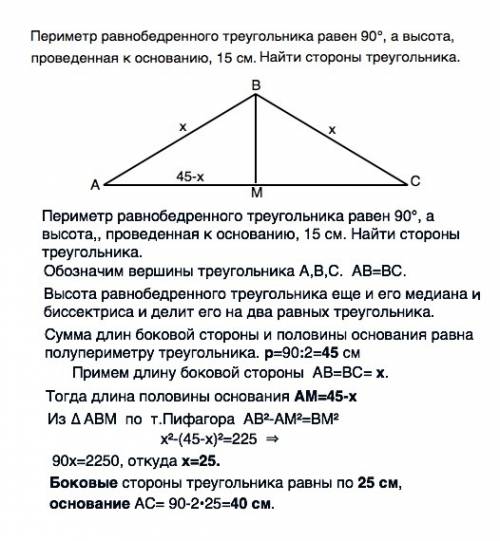
Периметр равнобедренного треугольника равен 90°, а высота,, проведенная к основанию, 15 см. Найти стороны треугольника.
Обозначим вершины треугольника А,В,С. АВ=ВС.
Высота равнобедренного треугольника еще и его медиана и биссектриса и делит его на два равных треугольника.
Сумма длин боковой стороны и половины основания равна полупериметру треугольника. р=90:2=45 см
Примем длину боковой стороны АВ=ВС= х.
Тогда длина половины основания АМ=45-х
Из ∆ АВМ по т.Пифагора АВ²-АМ²=ВМ²
х²-(45-х)²=225
90х=2250, откуда х=25.
Боковые стороны треугольника равны по 25 см,
основание АС= 90-2•25=40 см.
Х+90⁰+Х=360⁰
2Х=270⁰
Х=135⁰
Значит дуга ЕКН=135⁰, тогда дуга ЕАН=135⁰+90⁰=225⁰
Угол ЕАН=1\2ЕКН=67⁰30¹
Угол ЕКА=1\2ЕА=90⁰ (Любой вписанны угол, опирающийся на диаметор будет прямым)
Угол ЕКН вписан в окружность и опирается на дугу ЕАН, ⇒ ЕКН=1\2ЕАН=112⁰30¹(114 градусов и 30 минут - единицу я поставила вместо штриха)
ответ:
ЕКА=90⁰,
ЕАН=67⁰30¹,
ЕКН=112⁰30¹.