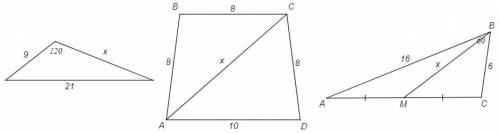
5)
21^2 =9^2 +x^2 -2*9*x*cos120 =>
x^2 +9x -360 =0 =>
x = -9 +√(81 +4*360) /2 =(39-9)/2 =15 (см) (x>0)
7)
теорема косинусов для △ABC и △ADC
∠B =180-∠D => cosB = -cosD
x^2 =8^2 +8^2 -2*8*8*cosB
x^2 =8^2 +10^2 -2*8*10*cosD
(x^2 -128)/(x^2 -164) = -4/5 =>
5x^2 -640 = -4x^2 +656 =>
x^2 =1296/9 => x=12 (см)
8)
AC^2 = 16^2 +6^2 -2*16*6*cos60 => AC=14
AM=MC=7
теорема косинусов для △AMB и △BMC
∠AMB =180-∠BMC => cosAMB = -cosBMC
16^2 =x^2 +7^2 -2*x*7*cosAMB
6^2 =x^2 +7^2 -2*x*7*cosBMC
(x^2 -207)/(x^2 +13) = -1 =>
2x^2 =194 => x=√97 (см)
реши это уравнение и найдешь n
n=15
2. сумма углов = 180 * (n - 2) = 180 * (5 - 2) = 540
4х + 5х + 6х + 7х + 8х = 30х
30х = 540
х = 18
8х = 144
3. Р= 12\/2
1 сторона = 3\/2
по т. пифагора найдем диагональ квадрата (например АВ) , которая является диаметром описанной окружности диаг=корень из(3\/2 в квадрате+3\/2 в квадрате)
диаг= \/36=6
диаметр= 2 радиусам, следовательно, r=3
4. В правильном треугольнике медианы делятся точкой пересечения в отношении 2:1, 2 части это радиус опис. окр, 1часть радиур впис окр, т.е 10√3 /2=5√3
5.внутренний угол равен 180 - (180 - 144)/2 = 180 - 18 = 162
сумма углов правильного многоугольника равна 180(n - 2)162n = 180n - 36018n = 360n = 20
Следовательно сумма углов равна 162*20 = 3240
8.Представь себе колесо, в нем восемь спиц, угол между ними 360/8=45 градусов
проводим высоту из центра колеса ( круга, 8угольника) к стороне 8угольника, таким образом получается прямоугольный треугольник с острым углом 45/2=22.5 градусов, один катет-эта высота, противолежащий катет- 0.5 метра, гипотенуза- радиус описанного круга.
Таким образом радиус равен 0.5/sin(22.5)=1.307м
Ну а площадь круга=ПИ*R*R=1.307*1.307*3.14=5.3 кв. м.