Так как дано, что многоугольник выпуклый, то сумма его внешних углов равна 360 градусам.
Каждый внешний угол равен по 90 градусам, тогда мы сможем узнать количество сторон. Для этого поделим сумму внешних углов на градусную меру каждого угла - 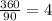
Итак, количество сторон = 4.
Но так как каждый внешний угол прямой, то и внутренние углы этого многоугольника тоже прямые. Тогда получается, что этот многоугольник - прямоугольник (все углы равны между собой).
Но так как у этого многоугольника равны все стороны (по условию) и углы, то это правильный четырёхугольник - квадрат.
ответ: квадрат.
Так как дано, что многоугольник выпуклый, то сумма его внешних углов равна 360 градусам.
Каждый внешний угол равен по 90 градусам, тогда мы сможем узнать количество сторон. Для этого поделим сумму внешних углов на градусную меру каждого угла - 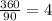
Итак, количество сторон = 4.
Но так как каждый внешний угол прямой, то и внутренние углы этого многоугольника тоже прямые. Тогда получается, что этот многоугольник - прямоугольник (все углы равны между собой).
Но так как у этого многоугольника равны все стороны (по условию) и углы, то это правильный четырёхугольник - квадрат.
ответ: квадрат.
---> радиусы обеих окружностей равны...
высота параллелограмма = 2 (диаметру окружностей)))
отрезок касательной к окружности (стороны параллелограмма))) -- это катет прямоугольного треугольника, в кот. второй катет = радиусу окружности...
тогда тангенс острого угла в этом треугольнике (этот угол -- половина угла параллелограмма))) tg(a) = 1 / V3 --- угол (а) = 30 градусов
---> один из углов параллелограмма = 60 градусов
второй угол параллелограмма = 120 градусов
на противоположной стороне параллелограмма отрезок стороны от вершины до точки касания будет равен (обозначим его х)))
tg(60) = 1 / x
x = 1 / tg(60) = 1 / V3 = V3 / 3
тогда вся сторона параллелограмма (к которой мы уже высоту построили из диаметра окружности))) = (V3 / 3) + 1 + 1 + V3 = ((2+V3)*3 + V3) / 3 = (6 + 4V3) / 3
Sпараллелограмма = 2*(6 + 4V3) / 3 = 4 + 8*V3 / 3