DOA = 70°. Дано в задаче.
BOC = DOA = 70°. Вертикальные углы равны (1).
DOC = 180° - 70° - 110°. Смежные углы в сумме дают 180° (2).
AOB = DOC = 110°. (1).
ODC = (180° - 110°) / 2 = 35°. Сумма углов треугольника равна 180° (3). Если треугольник равнобедренный, то углы при его основаниях равны (4).
ADO = 90° - 35° = 55°. Два угла составляют прямой угол (5).
OAD = ADO = 55°. (4).
OAB = 90° - 55° = 35°. (5).
OBA = OAB = 35°. (4).
OBC = 90° - 35° = 55°. (5).
OCB = OBC = 55°. (4).
Все остальные углы состоят из других и их можно посчитать по сумме. Например:
DAB = DAO + BAO = 55° + 35° = 90°.
ответ: 6√5 см
Объяснение:
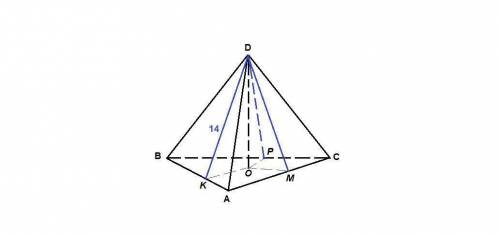
Пусть DO - высота пирамиды, DK, DM, DP - высоты боковых граней.
DK = DM = DP = 14 см по условию.
OK, OM и ОР - проекции наклонных, тогда они перпендикулярны сторонам треугольника АВС по теореме о трех перпендикулярах.
Если равны наклонные, проведенные из одной точки, то равны и их проекции, значит
ОК = ОМ = ОР, следовательно О - центр окружности, вписанной в ΔАВС, а ОК, ОМ и ОР - ее радиусы.
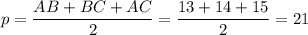
По формуле Герона
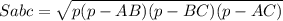
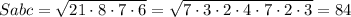 см²
см²
S = pr
84 = 21r
r = 4 см
ΔDKO: ∠DOK = 90°
по теореме Пифагора
DO = √(DK² - KO²) = √(196 - 16) = √180 = 6√5 см