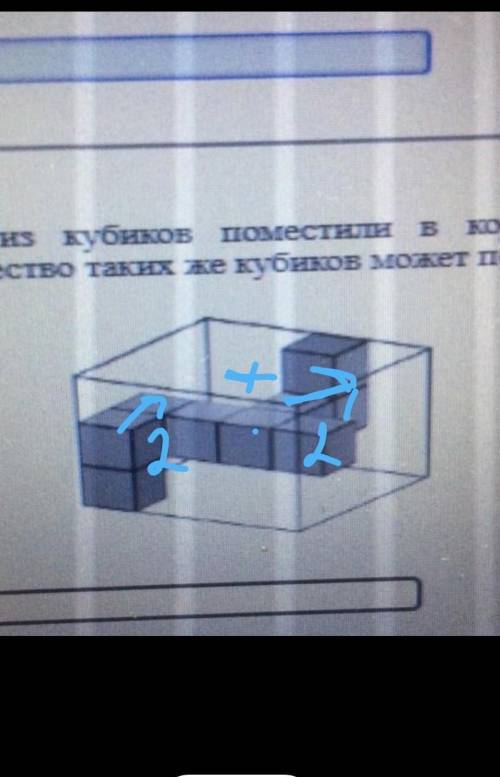
48 кубиков
Объяснение:
3*4*4=48 (V)
В параллелепипеде расположены кубики таким образом что видно какой из себя объем представляет он. по схеме мы можем понять что в длину 4 кубика. Дальше мы смотрим на высоту мы видим что в высоту вмещается 2 кубика но есть ещё место пустое, на высоте же 2 кубика проходят кубика вдоль длины и отходят на задний план и поднимаются на 1 выше окончательно. Из этого можно сделать вывод что он в высоту 3 кубика. В ширину же мы смотрим опять на кубике которые расположены на высоте 2 куба. я посчитала как показана на рисунке , вышло 4. Из этого всего мы считаем объем что и показывает сколько вмещает в себя кубиков параллелепипед.
96 АЕ = ЕК.
Докажите, что прямоугольник ABCD и треугольник AKD равновелики.
ответ : Равновеликими называются фигуры, имеющие равные площади.
Проведем КН⊥EF и рассмотрим треугольники АВЕ и КНЕ : ∠АВЕ = ∠КНЕ = 90°, АЕ = ЕК по условию, ∠АЕВ = ∠КЕН как вертикальные, ⇒ ΔАВЕ = ΔΔКНЕ по гипотенузе и острому углу.
Из равенства треугольников следует, что КН = АВ.
АВ = CD, значит КН = CD.
Рассмотрим треугольники KHF и DCF : ∠KHF = ∠DCF = 90°, KH = CD, ∠KFH = ∠DFC как вертикальные, значит ΔKHF = ΔDCF по катету и противолежащему острому углу.
Итак, Sabe = Skhe - зеленые треугольники, Skhf = Sdcf - желтые треугольники.
Площадь прямоугольника состоит из площади голубой трапеции, площади зеленого треугольника и площади желтого треугольника.
Из площадей таких же фигур состоит и площадь треугольника AKD, значитSabcd = Sakd.
Или можно записать все это в обозначениях : Sabcd = Saefd + Sabe + SdcfSakd = Saefd + Skeh + SkfhSabe = Skeh, Sdcf = Skfh, ⇒ Sabcd = Sakb.
Объяснение:
вот сам писал
Углы 1(А) и 4 внешний угол возле угла В слева( являются накрест лежащими углами при пересечении параллельных прямых а и АС секущей АВ, а углы 3(С) и 5внешний угол возле угла В справа — накрест лежащими углами при пересечении тех же параллельных прямых секущей ВС. Поэтому
∠ 4 = ∠ 1, ∠ 5 = ∠ 3. (1) Очевидно, сумма углов 4, 2 и 5 равна развернутому углу с вершиной В, т. е.
∠ 4 + ∠ 2 (В) + ∠ 5 = 180°. Отсюда, учитывая равенства (1), получаем:
∠ l + ∠ 2 + ∠ 3 = 180°, или ∠ A + ∠ B + ∠ C = 180°. Теорема доказана.