≈ 249,4 см²
Объяснение:
Задача:
В основе прямой призмы лежит прямоугольный треугольник с катетом 8 см и гипотенузой 10 см. Диагональ боковой грани, содержащая меньший из катетов, образует с плоскостью основания угол 60°. Найдите площадь полной поверхности призмы.
Дано:
а = 8 cм
c = 10 см
α = 60°
Найти:
S - площадь полной поверхности призмы
2-й катет b прямоугольного треугольника находится по теореме Пифагора с² = а² + b². Откуда
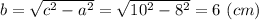
Этот катет b < a, и по условию является проекцией диагонали d боковой грани, содержащей меньший катет b, Поэтому угол между диагональю d и катетом b составляет α = 60°.
Высота призмы h = b · tg α = 6 · tg 60° = 6√3 (см).
Площадь боковой поверхности призмы
S бок = (а + b + с) · h = (8 + 6 + 10) · 6√3 = 144√3 (см²) ≈ 249,4 см²
Площадь оснований призмы
S осн = 2(0,5 ab) = ab = 8 · 6 = 48 (см²).
Площадь полной поверхности призмы
S полн = S бок + S осн = 249,4 + 48 = 297,4 (см²)
Площадь поверхности шара равна Sш=4πR²ш =92,2π