решение в подвеске))))))))))))))))))))
Пусть дан треугольник АВС, и пряммые АВ и АС параллельны плоскости Альфа. Пряммые АВ и АС пересекаются. Через них можно провести плоскость и причем одну. Пусть плоскость которая проходит через пряммые АВ и АС - плоскость Бэта. Тогда она параллельна плоскости Альфа, так как две пересекающиеся пряммые этой плоскости параллельны плоскости Альфа.
Далее. Две точки В и С принадлежат плоскости Бэта (так как принадлежат пряммые АВ и АС), значит и вся пряммая ВС принадлежит плоскости Бэта. Любая пряммая плоскости Бэта паралельна плосоксти Альфа (так плоскосит параллельны), в частности пряммая ВС параллельна плоскости Альфа.
ответ: третья пряммая тоже паралелльна плоскости
1) чтобы через две скрещивающиеся прямые построить две параллельные плоскости, необходимо:
- провести прямую с, пересекающую прямую b и параллельную прямой а
- провести прямую d, пересекающую прямую a и параллельную прямой b
Получится две пересекающиеся прямые, которые параллельны двум другим пересекающимся прямым, а значит эти пересекающиеся прямые лежат в плоскостях параллельных друг другу.
2) Третья сторона тоже параллельна плоскости
3) прямые MN и AD могут:
- пересекаться
- совпадать друг с другом (но при этом другие прямые трапеции не лежат в плоскости ромба)
- скрещиваться
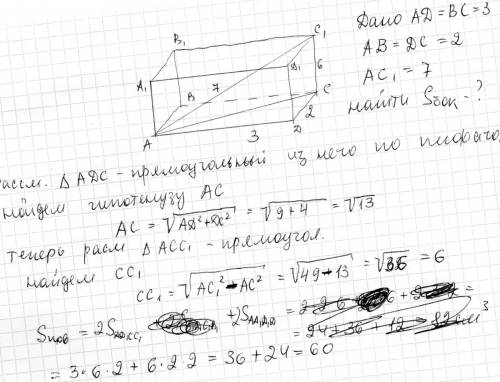
Значит есть формула d^2=a^2+b^2+c ^2
где d-диагональ
a,b,c-высота,ширина и длина
отсюда высота(c) равна c^2=d^2-a^2-b^2
c^2=49-4-9=36
c=6
Площадь боковой поверхности равна сумме боковых граней т.е. S=2ac+2ab=2*6*2+2*3*6=2*6*(2+3)=2*6*5=60