построем рисунок, в треугольнике ВСD: ВС=СD (т.к. шестиугольник правильный), угол равен 120 градусов, (по формуле для нахлждения угла в правильном многоугольнике а=180(n-2)/n), проведһм перпендикуляр СН, угол ВHC = (180-120)/2=30 (т.к. треугольник равнобедренный, углы при основании равны) следовательно, СН=0,5ВС = корень из 48 по полам=корень из двенадцати (после преобразования)
теперь ВН = (по теореме пифагора) корень из (48-12) = корень из 36 = 6
ВН равно HD (т.к. в равнобедренном треугольнике высота равна медиане) следовательно ВD=2BH = 6*2 = 12
Как то так!
ответ: вычисление всех диагоналей внизу на фото
Объяснение: в основании прямоугольного параллелепипеда лежит прямоугольник. Диагональ параллелепипеда вычисляется по формуле: Д=√(а²+b²+c²), - где a, b, c-его стороны. Диагонали параллелепипеда равны. Его грани также прямоугольники и диагонали одной грани и противоположных граней равны. Если провести диагонали у каждой боковой грани, то она разделит грань на 2 равных прямоугольных треугольника в которых стороны основания являются катетами а диагональ гипотенузой. Найдём диагонали граней по теореме Пифагора:
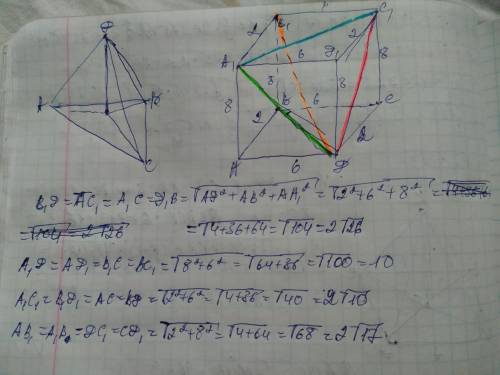
12; 12.
Объяснение:
Длина вектора определяется по формуле :
определяется по формуле :
Тогда получим :